Capítulo 5 Workflowsets & Stacking

Es común no sepamos ni remotamente cuál es el mejor modelo que podríamos implementar al iniciar un proyecto con datos que nunca antes hemos visto. Es posible que un profesional de datos deba seleccionar muchas combinaciones de modelos y preprocesadores. También es posible tener poco o ningún conocimiento a priori sobre qué método funcionará mejor con un nuevo conjunto de datos.

Una buena estrategia es dedicar un esfuerzo inicial a probar una variedad de enfoques de modelado, determinar qué funciona mejor y luego invertir tiempo adicional ajustando / optimizando un pequeño conjunto de modelos.

5.1 Múltiples recetas

Algunos modelos requieren predictores que se han centrado y escalado, por lo que algunos flujos de trabajo de modelos requerirán recetas con estos pasos de preprocesamiento. Para otros modelos, crear interacciones cuadráticas y bidireccionales. Para estos fines, creamos múltiples recetas:

library(tidymodels)

data(ames)

set.seed(4595)
ames_split <- initial_split(ames, prop = 0.75)
ames_train <- training(ames_split)
ames_test  <- testing(ames_split)
ames_folds <- vfold_cv(ames_train)

Receta Original

receta_original <- recipe(Sale_Price ~ . , data = ames_train) %>%
  step_unknown(Alley) %>%
  step_rename(Year_Remod = Year_Remod_Add) %>% 
  step_rename(ThirdSsn_Porch = Three_season_porch) %>% 
  step_ratio(Bedroom_AbvGr, denom = denom_vars(Gr_Liv_Area)) %>% 
  step_mutate(
    Age_House = Year_Sold - Year_Remod,
    TotalSF   = Gr_Liv_Area + Total_Bsmt_SF,
    AvgRoomSF   = Gr_Liv_Area / TotRms_AbvGrd,
    Pool = if_else(Pool_Area > 0, 1, 0),
    Exter_Cond = forcats::fct_collapse(Exter_Cond, Good = c("Typical", "Good", "Excellent"))) %>% 
  step_relevel(Exter_Cond, ref_level = "Good") %>% 
  step_normalize(all_predictors(), -all_nominal()) %>%
  step_dummy(all_nominal()) %>% 
  step_interact(~ Second_Flr_SF:First_Flr_SF) %>% 
  step_interact(~ matches("Bsmt_Cond"):TotRms_AbvGrd) %>% 
  step_rm(
    First_Flr_SF, Second_Flr_SF, Year_Remod,
    Bsmt_Full_Bath, Bsmt_Half_Bath, 
    Kitchen_AbvGr, BsmtFin_Type_1_Unf, 
    Total_Bsmt_SF, Kitchen_AbvGr, Pool_Area, 
    Gr_Liv_Area, Sale_Type_Oth, Sale_Type_VWD
  ) 

receta_original_prep <- receta_original %>% prep()

Receta KNN:

receta_knn <- recipe(Sale_Price ~ . , data = ames_train) %>%
  step_unknown(Alley) %>%
  step_unknown(Pool_QC) %>%
  step_unknown(Misc_Feature) %>%
  step_unknown(Fence) %>%
  step_unknown(Garage_Finish) %>%
  step_unknown(Garage_Cond) %>%
  step_unknown(Garage_Type) %>%
  step_unknown(Bsmt_Exposure) %>%
  step_unknown(Bsmt_Cond) %>%
  step_unknown(BsmtFin_Type_1) %>%
  step_unknown(BsmtFin_Type_2) %>%
  step_unknown(Mas_Vnr_Type) %>%
  step_unknown(Electrical) %>%
  step_impute_knn(
    Mas_Vnr_Area, Lot_Frontage, 
    impute_with= all_predictors(),
    neighbors = 5) %>%
  step_rename(Year_Remod = Year_Remod_Add) %>% 
  step_rename(ThirdSsn_Porch = Three_season_porch) %>% 
  step_ratio(Bedroom_AbvGr, denom = denom_vars(Gr_Liv_Area)) %>% 
  step_mutate(
    Age_House = Year_Sold - Year_Remod,
    TotalSF   = Gr_Liv_Area + Total_Bsmt_SF,
    AvgRoomSF   = Gr_Liv_Area / TotRms_AbvGrd,
    Pool = if_else(Pool_Area > 0, 1, 0),
    Exter_Cond = forcats::fct_collapse(Exter_Cond, Good = c("Typical", "Good", "Excellent"))) %>% 
  step_relevel(Exter_Cond, ref_level = "Good") %>% 
  step_normalize(all_predictors(), -all_nominal()) %>%
  step_dummy(all_nominal()) %>% 
  step_interact(~ Second_Flr_SF:First_Flr_SF) %>% 
  step_interact(~ matches("Bsmt_Cond"):TotRms_AbvGrd) 

receta_knn_prep <- receta_knn %>% prep()

Receta Grande:

receta_grande <- recipe(Sale_Price ~ . , data = ames_train) %>%
  step_unknown(Alley) %>%
  step_unknown(Fence) %>%
  step_unknown(Garage_Type) %>%
  step_unknown(Garage_Finish) %>%
  step_unknown(Garage_Cond) %>%
  step_unknown(Bsmt_Cond) %>%
  step_unknown(Bsmt_Exposure) %>%
  step_unknown(BsmtFin_Type_1) %>%
  step_unknown(BsmtFin_Type_2) %>%
  step_unknown(Mas_Vnr_Type) %>%
  step_unknown(Electrical) %>%
  step_unknown(Heating_QC) %>%
  step_unknown(Pool_QC) %>% 
  step_impute_knn(
    Mas_Vnr_Area, Lot_Frontage, 
    impute_with= all_predictors(),
    neighbors = 5) %>%
  step_rename(Year_Remod = Year_Remod_Add) %>% 
  step_rename(ThirdSsn_Porch = Three_season_porch) %>% 
  step_ratio(Bedroom_AbvGr, denom = denom_vars(Gr_Liv_Area)) %>% 
  step_ratio(Second_Flr_SF, denom = denom_vars(First_Flr_SF)) %>% 
  step_mutate(
    TotalBaths = Full_Bath + Bsmt_Full_Bath + 0.5 * (Half_Bath + Bsmt_Half_Bath),
    Age_House = Year_Sold - Year_Remod,
    TotalSF = Gr_Liv_Area + Total_Bsmt_SF,
    Porc_H_over_TotalSF = (TotalSF / Lot_Area) * 100,
    AvgRoomSF = Gr_Liv_Area / TotRms_AbvGrd,
    Porch_SF = Enclosed_Porch + ThirdSsn_Porch + Open_Porch_SF,
    Porch = factor(Porch_SF > 0),
    Pool = if_else(Pool_Area > 0,1,0),
    Exter_Cond = forcats::fct_collapse(Exter_Cond, Good = c("Typical", "Good", "Excellent")),
    Condition_1 = forcats::fct_collapse(
      Condition_1, 
      Artery_Feedr = c("Feedr", "Artery"), 
      Railr = c("RRAn", "RRNn", "RRNe", "RRAe"),
      Norm = "Norm",
      Pos = c("PosN", "PosA")), 
    Land_Slope = forcats::fct_collapse(Land_Slope, Mod_Sev = c("Mod", "Sev")),
    Land_Contour = forcats::fct_collapse(Land_Contour, Low_HLS = c("Low","HLS"), Bnk_Lvl = c("Lvl","Bnk")),
    Lot_Shape = forcats::fct_collapse(Lot_Shape, IRREG = c("Slightly_Irregular", "Moderately_Irregular", "Irregular")),
    Bsmt_Cond = forcats::fct_collapse(Bsmt_Cond, Exc = c("Good", "Excellent")),
    BsmtFin_Type_1 = forcats::fct_collapse(BsmtFin_Type_1, Rec_BLQ = c("Rec", "BLQ")),
    BsmtFin_Type_2 = forcats::fct_collapse(BsmtFin_Type_2, Rec_BLQ = c("Rec", "BLQ","LwQ")),
    Neighborhood = forcats::fct_collapse(
      Neighborhood, 
      NoRidge_GrnHill = c("Northridge", "Green_Hills"),
      Crawfor_Greens = c("Crawford", "Greens"),
      Blueste_Mitchel = c("Blueste", "Mitchell"),
      Blmngtn_CollgCr = c("Bloomington_Heights", "College_Creek"),
      NPkVill_NAmes = c("Northpark_Villa", "North_Ames"),
      Veenker_StoneBr = c("Veenker", "Stone_Brook"),
      BrDale_IDOTRR = c("Briardale", "Iowa_DOT_and_Rail_Road"),
      SWISU_Sawyer = c("South_and_West_of_Iowa_State_University", "Sawyer"),
      ClearCr_Somerst = c("Clear_Creek", "Somerset")),
    Heating = forcats::fct_collapse(
      Heating, Grav_Wall = c("Grav", "Wall"),
      GasA_W = c("GasA", "GasW", "OthW")),
    MS_Zoning = forcats::fct_collapse(
      MS_Zoning, I_R_M_H = c("Residential_Medium_Density", "I_all", "Residential_High_Density" )),
    Bldg_Type = forcats::fct_collapse(Bldg_Type, Du_Tu = c("Duplex", "Twnhs")),
    Foundation = forcats::fct_collapse(Foundation, Wood_Stone = c("Wood", "Stone")),
    Functional = forcats::fct_collapse(
      Functional, Min = c("Min1", "Min2"), Maj = c("Maj1", "Maj2", "Mod"))) %>% 
  step_relevel(Exter_Cond, ref_level = "Good") %>% 
  step_relevel(Condition_1, ref_level = "Norm") %>%
  step_normalize(all_predictors(), -all_nominal()) %>%
  step_dummy(all_nominal()) %>% 
  step_interact(~ Second_Flr_SF:Bedroom_AbvGr) %>%
  step_interact(~ TotalSF:TotRms_AbvGrd) %>%
  step_interact(~ Age_House:TotRms_AbvGrd) %>%
  step_interact(~ Second_Flr_SF:First_Flr_SF) %>% 
  step_interact(~ matches("Bsmt_Cond"):TotRms_AbvGrd) %>% 
  step_interact(~ matches("BsmtFin_Type_1"):BsmtFin_SF_1) %>% 
  step_interact(~ matches("BsmtFin_Type_1"):Total_Bsmt_SF) %>% 
  step_interact(~ matches("Heating_QC"):TotRms_AbvGrd) %>% 
  step_interact(~ matches("Heating_QC"):TotalSF) %>%
  step_interact(~ matches("Heating_QC"):Second_Flr_SF) %>%
  step_interact(~ matches("Neighborhood"):matches("Condition_1")) %>% 
  step_rm(
    First_Flr_SF, Second_Flr_SF, Year_Remod,
    Bsmt_Full_Bath, Bsmt_Half_Bath, 
    Kitchen_AbvGr, BsmtFin_Type_1_Unf, 
    Total_Bsmt_SF, Kitchen_AbvGr, Pool_Area, 
    Gr_Liv_Area, Porch_SF,
    Sale_Type_Oth, Sale_Type_VWD
  )

receta_grande_prep <- receta_grande %>% prep()

5.2 Múltiples modelos

Una vez que tenemos suficientes recetas, podemos experimentar con múltiples modelos para poner a prueba. Usaremos los modelos que hemos aprendido a implementar en todo el curso:

library(rules)
library(baguette)
library(tune)

elasticnet_model <- linear_reg(
  mode = "regression",
  penalty = tune(),
  mixture = tune()) %>%
  set_engine("glmnet") 

knn_model <- nearest_neighbor(
  mode = "regression",
  neighbors = tune("K"),
  dist_power = tune(),
  weight_func = tune()) %>%
  set_engine("kknn")

rforest_model <- rand_forest(
  mode = "regression",
  trees = 1000,
  mtry = tune(),
  min_n = tune()) %>%
  set_engine(
    "ranger",
    importance = "impurity"
  )

svm_rbf_model <- svm_rbf(
  cost = tune(),
  rbf_sigma = tune(),
  margin = tune()) %>%
  set_engine("kernlab") %>%
  set_mode("regression")

xgboost_model <- boost_tree(
  mode = "regression",
  trees = 1000,
  tree_depth = tune(),
  min_n = tune(),
  loss_reduction = tune(),
  sample_size = tune(),
  mtry = tune(),
  learn_rate = tune()) %>%
  set_engine(
    "xgboost",
    importance = "impurity"
  )

¿Cómo podemos hacer coincidir estos modelos con las recetas desarrolladas, ajustarlos y luego evaluar su rendimiento de manera eficiente? WORKFLOWSETS ofrece una solución.

5.3 Creación de workflowset

Los conjuntos de flujo de trabajo toman listas nombradas de preprocesadores y especificaciones de modelos y las combinan en un objeto que contiene múltiples flujos de trabajo.

Como primer ejemplo de conjunto de flujo de trabajo, combinemos las recetas creadas en la sección anterior.

workflow_set_models <- workflow_set(
  preproc = list(
    receta_original = receta_original_prep, 
    receta_knn = receta_knn_prep,
    receta_grande = receta_grande_prep
    ),
  models = list(
    elasticnet = elasticnet_model,
    knn = knn_model,
    rf = rforest_model,
    svm_rbf = svm_rbf_model,
    boost = xgboost_model
    )
  )

5.4 Ajuste y evaluación de modelos

Casi todos estos flujos de trabajo contienen parámetros de ajuste. Para evaluar su rendimiento, podemos utilizar las funciones estándar de ajuste o remuestreo (por ejemplo, tune_grid()).

La función workflow_map() aplicará la misma función a todos los flujos de trabajo del conjunto; el valor predeterminado es tune_grid().

A continuación se declaran los parámetros para cada modelo y el grid:

elasticnet_params <- elasticnet_model %>%
  parameters() %>%
  update(
    penalty = penalty(
      range = c(-2, 3),
      trans = log10_trans()),
    mixture = dials::mixture(range = c(0, 1))
  )

knn_params <- knn_model %>%
  parameters() %>%
  update(
    K = dials::neighbors(c(5, 80)),
    dist_power = dist_power(range = c(1, 3)),
    weight_func = weight_func(values = c("rectangular", "inv", "gaussian", "cos"))
  )

rforest_params <- rforest_model %>%
  parameters() %>%
  update(
    mtry = finalize(mtry(range = c(15, 80))),
    min_n = min_n(range = c(3,15))
  )

svm_rbf_params <- svm_rbf_model %>%
  parameters() %>%
  update(
    cost = cost(c(0, 0.5)),
    rbf_sigma = rbf_sigma(c(-3, 3)),
    margin = svm_margin(c(-2, 2))
  )

xgboost_params <- xgboost_model %>%
  parameters() %>%
  update(
    min_n = min_n(range = c(5,15)),
    mtry = finalize(mtry(range = c(5, 80))),
    tree_depth = tree_depth(range = c(3, 50)),
    loss_reduction = loss_reduction(range = c(-10, 1.5), trans = log10_trans()),
    learn_rate = learn_rate(range = c(-6, -0.25), trans = log10_trans()),
    sample_size = sample_prop()
  )

# Declaración del grid
workflow_tunning_set_models <- workflow_set_models %>%
  option_add(param_info = elasticnet_params, id = "elasticnet") %>% 
  option_add(param_info = knn_params, id = "knn") %>%
  option_add(param_info = rforest_params, id = "rf") %>%
  option_add(param_info = svm_rbf_params, id = "svm_rbf") %>%
  option_add(param_info = xgboost_params, id = "xgboost")

workflow_tunning_set_models

## # A workflow set/tibble: 15 × 4
##    wflow_id                   info             option    result    
##    <chr>                      <list>           <list>    <list>    
##  1 receta_original_elasticnet <tibble [1 × 4]> <opts[0]> <list [0]>
##  2 receta_original_knn        <tibble [1 × 4]> <opts[0]> <list [0]>
##  3 receta_original_rf         <tibble [1 × 4]> <opts[0]> <list [0]>
##  4 receta_original_svm_rbf    <tibble [1 × 4]> <opts[0]> <list [0]>
##  5 receta_original_boost      <tibble [1 × 4]> <opts[0]> <list [0]>
##  6 receta_knn_elasticnet      <tibble [1 × 4]> <opts[0]> <list [0]>
##  7 receta_knn_knn             <tibble [1 × 4]> <opts[0]> <list [0]>
##  8 receta_knn_rf              <tibble [1 × 4]> <opts[0]> <list [0]>
##  9 receta_knn_svm_rbf         <tibble [1 × 4]> <opts[0]> <list [0]>
## 10 receta_knn_boost           <tibble [1 × 4]> <opts[0]> <list [0]>
## 11 receta_grande_elasticnet   <tibble [1 × 4]> <opts[0]> <list [0]>
## 12 receta_grande_knn          <tibble [1 × 4]> <opts[0]> <list [0]>
## 13 receta_grande_rf           <tibble [1 × 4]> <opts[0]> <list [0]>
## 14 receta_grande_svm_rbf      <tibble [1 × 4]> <opts[0]> <list [0]>
## 15 receta_grande_boost        <tibble [1 × 4]> <opts[0]> <list [0]>

Dado que el preprocesador contiene más de una entrada, la función crea todas las combinaciones de preprocesadores y modelos.

info: Contiene un tibble con algunos identificadores y el objeto de flujo de trabajo.
option: Es un marcador de posición para cualquier argumento que se utilice cuando evaluamos el flujo de trabajo.
result: Es un marcador de posición para la salida de las funciones de ajuste o remuestreo.

Para este ejemplo, la búsqueda del grid se aplica al flujo de trabajo.

library(doParallel)

UseCores <- detectCores() - 1
cluster <- makeCluster(UseCores)
registerDoParallel(cluster)

grid_ctrl <- control_grid(
    save_pred = TRUE,
    save_workflow = TRUE,
    parallel_over = "everything"
)

set.seed(536)
tunning_models_result <- workflow_tunning_set_models %>%
  workflow_map(
    fn = "tune_grid",
    seed = 20220603,
    resamples = ames_folds,
    grid = 100,
    metrics =  metric_set(rmse, mae, mape, rsq),
    control = grid_ctrl,
    verbose = TRUE
  )

stopCluster(cluster)

tunning_models_result %>% saveRDS("models/ensemble_model.rds")

tunning_models_result <- readRDS("models/ensemble_model.rds")

tunning_models_result %>%
  rank_results(select_best = T) %>%
  select(-c(.config, n, preprocessor, std_err)) %>%
  pivot_wider(names_from = .metric, values_from = mean)

## # A tibble: 15 × 7
##    wflow_id                   model             rank    mae  mape   rmse   rsq
##    <chr>                      <chr>            <int>  <dbl> <dbl>  <dbl> <dbl>
##  1 receta_knn_boost           boost_tree           1 16614.  10.4 25425. 0.900
##  2 receta_knn_rf              rand_forest          2 17766.  11.1 28489. 0.877
##  3 receta_knn_svm_rbf         svm_rbf              3 17985.  11.3 29103. 0.865
##  4 receta_knn_knn             nearest_neighbor     4 19471.  11.6 30465. 0.861
##  5 receta_original_boost      boost_tree           5 20019.  12.2 30569. 0.856
##  6 receta_grande_boost        boost_tree           6 20019.  12.2 30569. 0.856
##  7 receta_original_rf         rand_forest          7 21058.  12.9 33599. 0.828
##  8 receta_grande_rf           rand_forest          8 21058.  12.9 33599. 0.828
##  9 receta_grande_knn          nearest_neighbor     9 22561.  13.0 35353. 0.817
## 10 receta_original_knn        nearest_neighbor    10 22561.  13.0 35353. 0.817
## 11 receta_grande_svm_rbf      svm_rbf             11 22839.  13.8 35431. 0.807
## 12 receta_original_svm_rbf    svm_rbf             12 22839.  13.8 35431. 0.807
## 13 receta_knn_elasticnet      linear_reg          13 24196.  14.7 39880. 0.756
## 14 receta_grande_elasticnet   linear_reg          14 30129.  18.4 44124. 0.694
## 15 receta_original_elasticnet linear_reg          15 30129.  18.4 44124. 0.694

autoplot(
  tunning_models_result,
  rank_metric = "rsq",
  metric = "rsq",   
  select_best = F) +   
  lims(y = c(0, 1)) +
  ggtitle("Model Comparisson")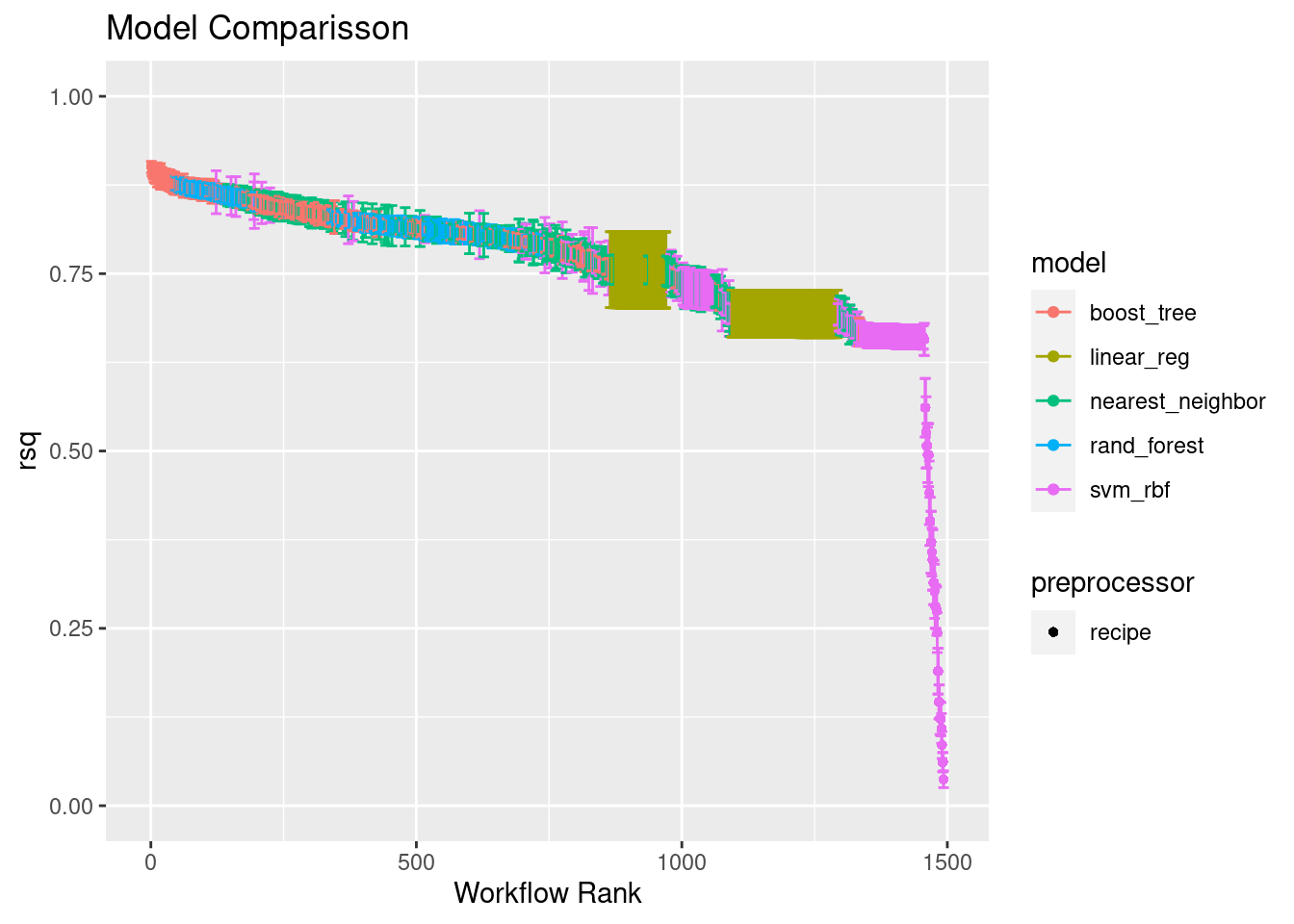

autoplot(
  tunning_models_result,
  rank_metric = "rsq",
  metric = "rsq",   
  select_best = T) +
  geom_text(aes(y = mean - 0.10 , label = wflow_id), angle = 90, hjust = 1) +
  lims(y = c(0, 1)) +
  ggtitle("Model Comparisson")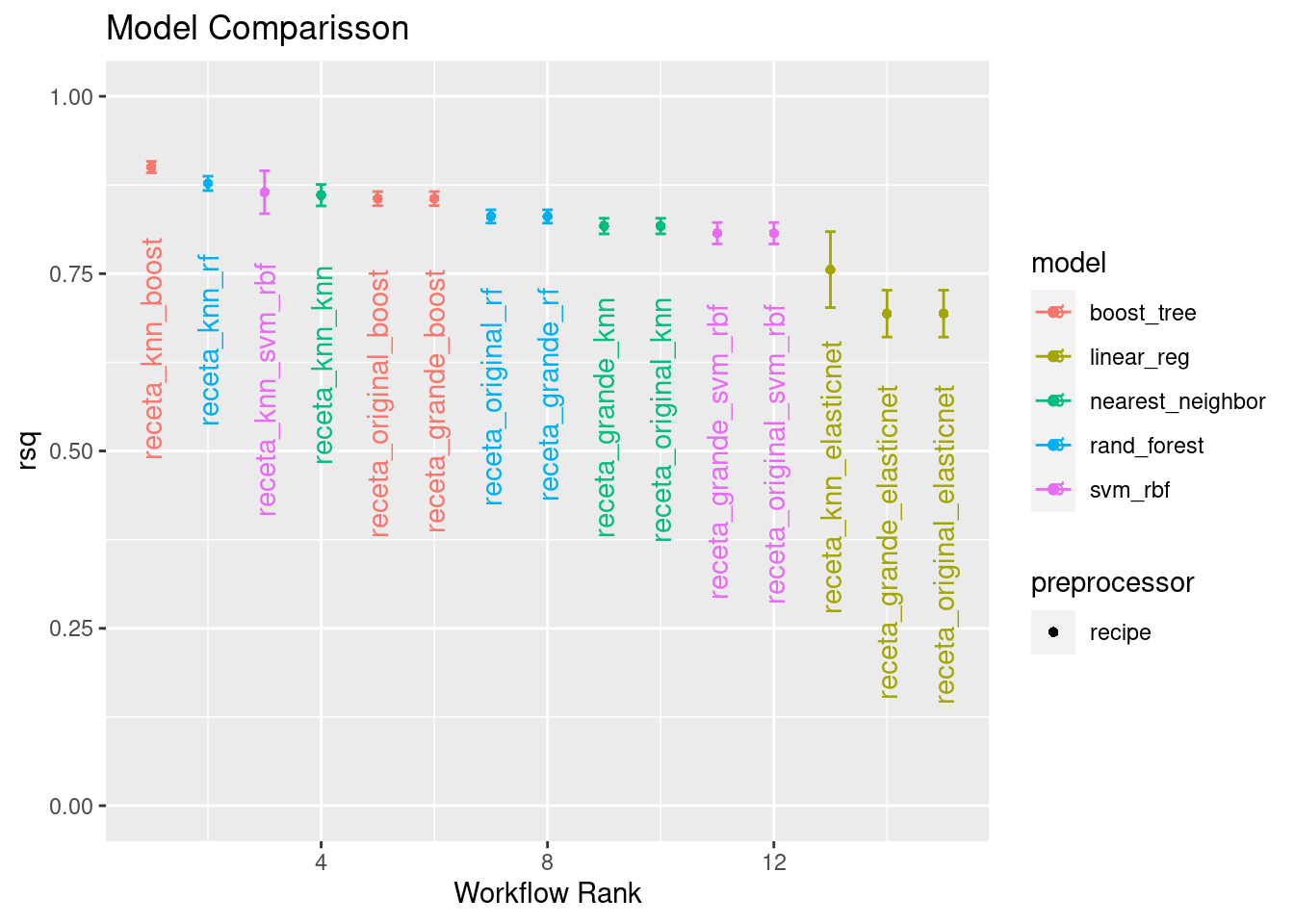

5.5 Extracción de modelos

Una vez que hemos realizado una exploración sobre el desempeño de todas las combinaciones de preprocesamientos con modelos, es posible tomar varios caminos hacia adelante. Algunas de las opciones más comunes son:

Realizar múltiples iteraciones de modificaciones a las recetas para extraer lo mejor de cada una.
Realizar mejoras a los hiperparámetros.
Eliminar modelos y/o recetas que no tuvieron buen desempeño.
Crear un modelo a partir de la combinación de los modelos más competentes.

Para empezar, se realiza una exploración del resultado del desempeño de los mejores modelos y los hiperparámetros usado en cada caso.

Resultados de XGBoost

tunning_models_result %>% 
  extract_workflow_set_result("receta_knn_boost") %>%
  autoplot(metric = "rsq")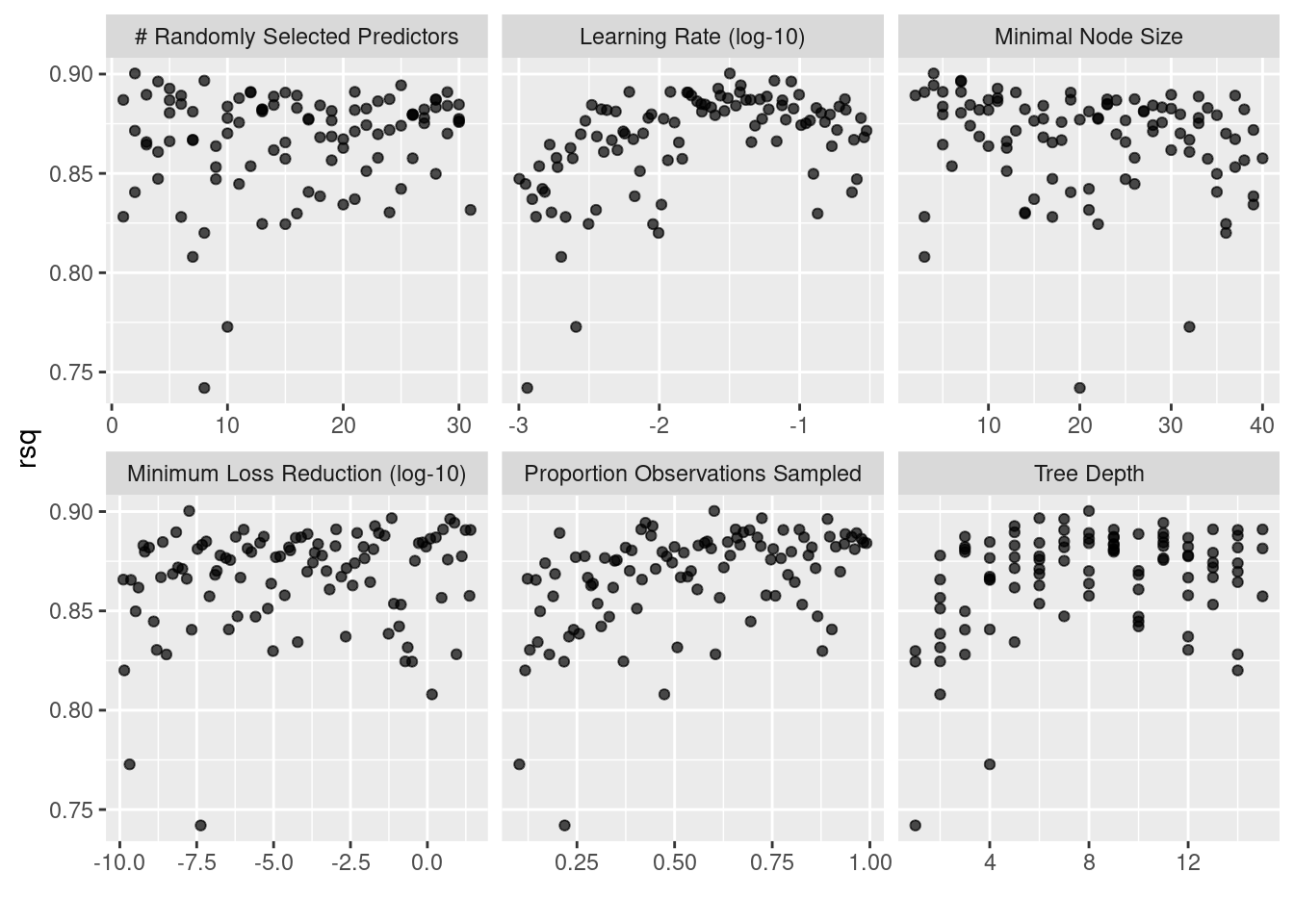

tunning_models_result %>% 
  extract_workflow_set_result("receta_knn_boost") %>%
  show_best(n = 10, metric = "rsq") %>% 
  select(-c(.estimator, .metric, .config, n))

## # A tibble: 10 × 8
##     mtry min_n tree_depth learn_rate loss_reduction sample_size  mean std_err
##    <int> <int>      <int>      <dbl>          <dbl>       <dbl> <dbl>   <dbl>
##  1     2     4          8    0.0318    0.0000000180       0.601 0.900 0.00487
##  2     8     7          6    0.0661    0.0692             0.723 0.897 0.00537
##  3     4     7          7    0.0871    5.50               0.892 0.896 0.00493
##  4    25     4         11    0.0381    7.61               0.425 0.894 0.00596
##  5     5    11          5    0.0263    0.0198             0.444 0.893 0.00581
##  6    21     5         13    0.0120    0.00108            0.415 0.891 0.00724
##  7    12     7         15    0.00611   3.24               0.656 0.891 0.00730
##  8    29     3          9    0.0375    0.00000107         0.820 0.891 0.00419
##  9    12    13         14    0.0158   25.3                0.778 0.891 0.00825
## 10    15    19          7    0.0161   17.5                0.692 0.891 0.00767

Resultados de Ranfom Forest

tunning_models_result %>% 
  extract_workflow_set_result("receta_knn_rf") %>%
  autoplot(metric = "rmse")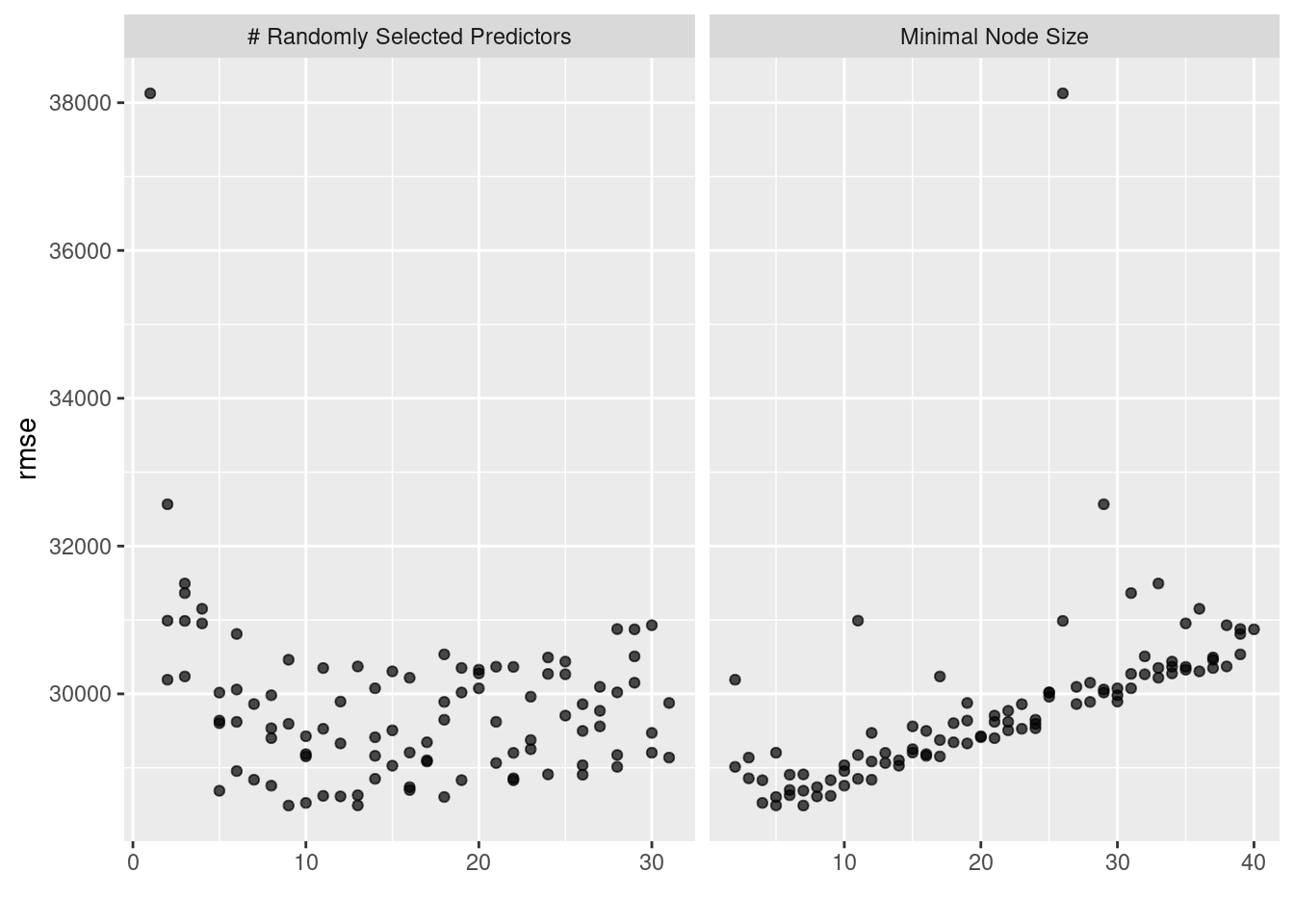

tunning_models_result %>% 
  extract_workflow_set_result("receta_knn_rf") %>%
  show_best(n = 10, metric = "rmse") %>% 
  select(-c(.estimator, .metric, .config, n))

## # A tibble: 10 × 4
##     mtry min_n   mean std_err
##    <int> <int>  <dbl>   <dbl>
##  1     9     7 28489.   1010.
##  2    13     5 28491.    883.
##  3    10     4 28524.    970.
##  4    18     5 28604.    882.
##  5    12     8 28613.    947.
##  6    11     9 28620.    939.
##  7    13     6 28628.    928.
##  8     5     7 28689.   1052.
##  9    16     6 28699.    920.
## 10    16     8 28737.    912.

5.5.1 Selección de modelo

Habiendo determinado los hiperparámetros adecuados para la configuración del modelo, procedemos a seleccionar la configuración adecuada para nosotros. Estos pasos son los mismos que corresponden a la selección del modelo con un único workflow.

Mejor modelo XGBoost

best_xgb_model <- tunning_models_result %>%
 extract_workflow_set_result("receta_knn_boost") %>%
 select_best(metric = "rsq", "rsq")

best_xgb_model %>% 
  mutate_all(as.character) %>% 
  pivot_longer(everything(), names_to = "metric", values_to = "value")

## # A tibble: 7 × 2
##   metric         value                 
##   <chr>          <chr>                 
## 1 mtry           2                     
## 2 min_n          4                     
## 3 tree_depth     8                     
## 4 learn_rate     0.0318069757974226    
## 5 loss_reduction 1.8022375282862e-08   
## 6 sample_size    0.60145520768594      
## 7 .config        Preprocessor1_Model058

Mejor modelo XGBoost a menos de una desviación estandar

best_regularized_xgb_model_1se <- tunning_models_result %>%
  extract_workflow_set_result("receta_knn_boost") %>%
  select_by_one_std_err(metric = "rsq", "rsq")

best_regularized_xgb_model_1se %>% 
  mutate_all(as.character) %>% 
  pivot_longer(everything(), names_to = "metric", values_to = "value")

## # A tibble: 14 × 2
##    metric         value                 
##    <chr>          <chr>                 
##  1 mtry           8                     
##  2 min_n          7                     
##  3 tree_depth     6                     
##  4 learn_rate     0.0660688823690034    
##  5 loss_reduction 0.0691664318630444    
##  6 sample_size    0.723484068220947     
##  7 .metric        rsq                   
##  8 .estimator     standard              
##  9 mean           0.896674936544582     
## 10 n              10                    
## 11 std_err        0.00536531804472105   
## 12 .config        Preprocessor1_Model035
## 13 .best          0.900303988301004     
## 14 .bound         0.895438860790247

Mejor modelo XGBoost a menos de un porcentaje fijo

best_regularized_xgb_model_pct <- tunning_models_result %>%
  extract_workflow_set_result("receta_knn_boost") %>%
  select_by_pct_loss(metric = "rsq", "rsq", limit = 10)

best_regularized_xgb_model_pct %>% 
  mutate_all(as.character) %>% 
  pivot_longer(everything(), names_to = "metric", values_to = "value")

## # A tibble: 14 × 2
##    metric         value                 
##    <chr>          <chr>                 
##  1 mtry           13                    
##  2 min_n          36                    
##  3 tree_depth     2                     
##  4 learn_rate     0.00313559984945049   
##  5 loss_reduction 0.190594567355415     
##  6 sample_size    0.36900916616735      
##  7 .metric        rsq                   
##  8 .estimator     standard              
##  9 mean           0.824569900806526     
## 10 n              10                    
## 11 std_err        0.00788602755362551   
## 12 .config        Preprocessor1_Model030
## 13 .best          0.900303988301004     
## 14 .loss          8.41205731381887

Ajuste del modelo seleccionado

final_regularized_xgb_model <- tunning_models_result %>%
  extract_workflow("receta_knn_boost") %>%
  finalize_workflow(best_regularized_xgb_model_1se) %>%
  parsnip::fit(data = ames_train)

## [01:07:31] WARNING: amalgamation/../src/learner.cc:627: 
## Parameters: { "importance" } might not be used.
## 
##   This could be a false alarm, with some parameters getting used by language bindings but
##   then being mistakenly passed down to XGBoost core, or some parameter actually being used
##   but getting flagged wrongly here. Please open an issue if you find any such cases.

final_regularized_xgb_model

## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: boost_tree()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 23 Recipe Steps
## 
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • step_unknown()
## • ...
## • and 13 more steps.
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## ##### xgb.Booster
## raw: 2.6 Mb 
## call:
##   xgboost::xgb.train(params = list(eta = 0.0660688823690034, max_depth = 6L, 
##     gamma = 0.0691664318630444, colsample_bytree = 1, colsample_bynode = 0.258064516129032, 
##     min_child_weight = 7L, subsample = 0.723484068220947, objective = "reg:squarederror"), 
##     data = x$data, nrounds = 1000, watchlist = x$watchlist, verbose = 0, 
##     importance = "impurity", nthread = 1)
## params (as set within xgb.train):
##   eta = "0.0660688823690034", max_depth = "6", gamma = "0.0691664318630444", colsample_bytree = "1", colsample_bynode = "0.258064516129032", min_child_weight = "7", subsample = "0.723484068220947", objective = "reg:squarederror", importance = "impurity", nthread = "1", validate_parameters = "TRUE"
## xgb.attributes:
##   niter
## callbacks:
##   cb.evaluation.log()
## # of features: 31 
## niter: 1000
## nfeatures : 31 
## evaluation_log:
##     iter training_rmse
##        1    184947.832
##        2    173406.092
## ---                   
##      999      1720.214
##     1000      1717.597

Como hemos hablado anteriormente, este último objeto es el modelo final entrenado, el cual contiene toda la información del pre-procesamiento de datos, por lo que en caso de ponerse en producción el modelo, sólo se necesita de este último elemento para poder realizar nuevas predicciones.

Es importante validar que hayamos hecho un uso correcto de las variables predictivas. En este momento es posible detectar variables que no estén aportando valor o variables que no debiéramos estar usando debido a que cometeríamos data leakage. Para enfrentar esto, ayuda estimar y ordenar el valor de importancia del modelo

library(vip)

final_regularized_xgb_model %>%
  extract_fit_parsnip() %>%
  vip::vip(num_features = 25) + 
  ggtitle("Importancia de las variables")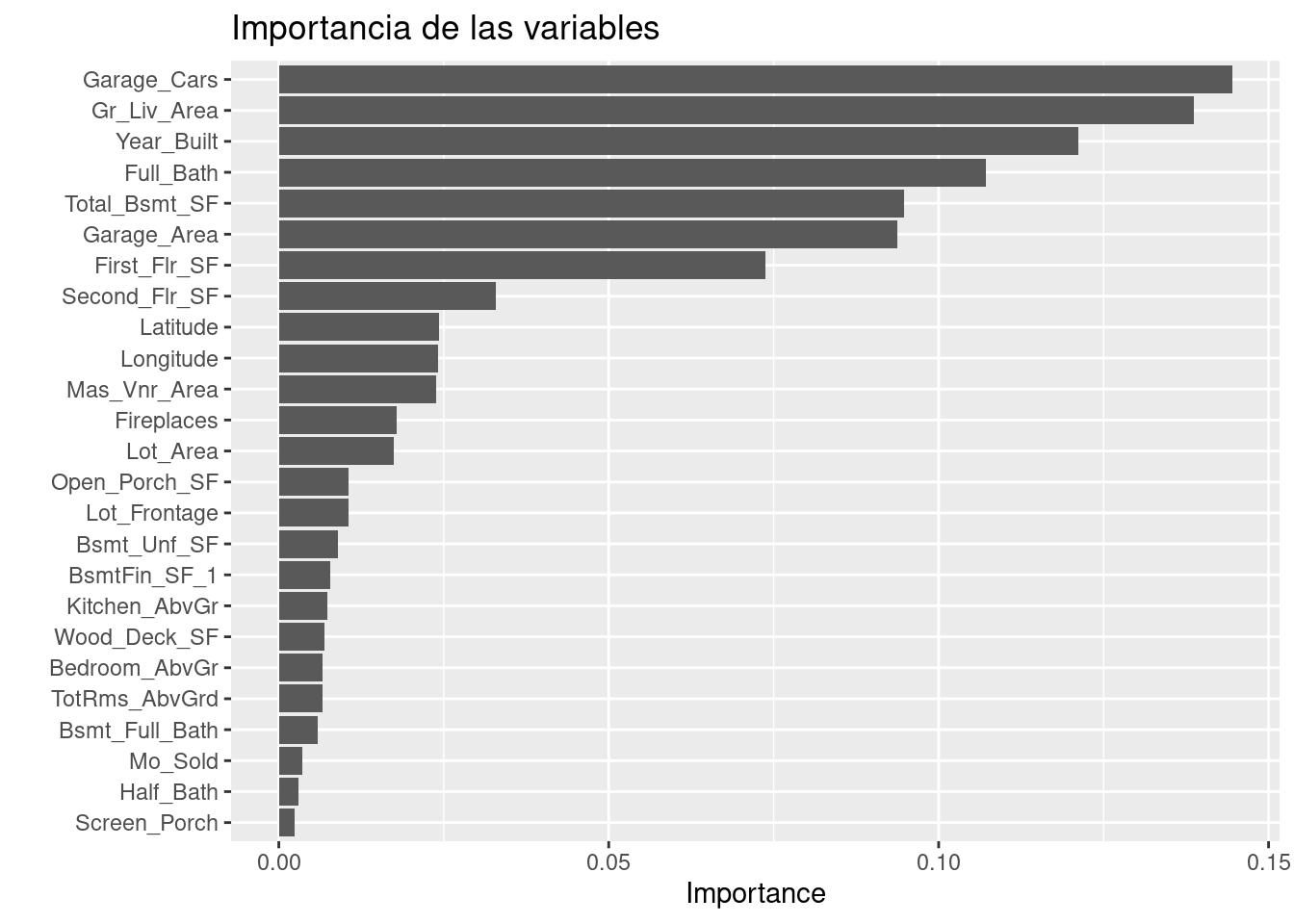

Por último… Imaginemos por un momento que pasa un mes de tiempo desde que hicimos nuestro modelo, es hora de ponerlo a prueba prediciendo valores de nuevos elementos:

results <- predict(final_regularized_xgb_model, ames_test) %>% 
  dplyr::bind_cols(truth = ames_test$Sale_Price) %>% 
  dplyr::rename(pred_xgb_reg = .pred, Sale_Price = truth)

head(results)

## # A tibble: 6 × 2
##   pred_xgb_reg Sale_Price
##          <dbl>      <int>
## 1      131972.     105000
## 2      175629.     185000
## 3      176203.     180400
## 4      106614.     141000
## 5      238267.     210000
## 6      213937.     216000

multi_metric <- metric_set(rmse, rsq, mae, mape, ccc)
multi_metric(results, truth = Sale_Price, estimate = pred_xgb_reg) %>% 
  mutate(.estimate = round(.estimate, 2))

## # A tibble: 5 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard    26851.  
## 2 rsq     standard        0.89
## 3 mae     standard    17078.  
## 4 mape    standard       10.5 
## 5 ccc     standard        0.94

results %>% 
  ggplot(aes(x = pred_xgb_reg, y = Sale_Price)) +
  geom_point() +
  geom_abline(color = "red") +
  xlab("Prediction") +
  ylab("Observation") +
  ggtitle("Comparisson")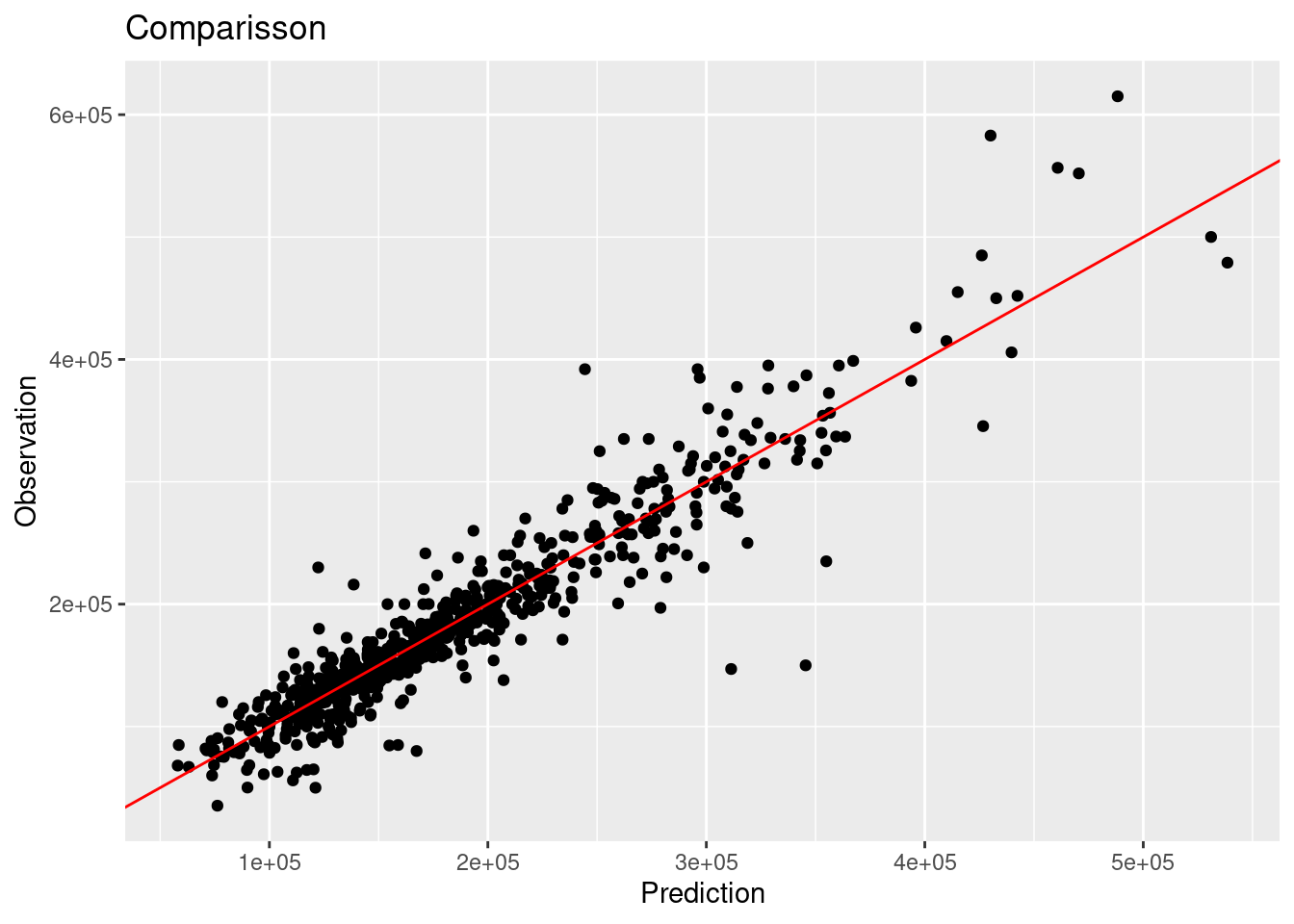

5.6 Métodos de carrera

Un problema con la búsqueda del grid es que todos los modelos deben ajustarse en todos los remuestreos antes de que se puedan evaluar los parámetros de ajuste.

En machine learning, el conjunto de técnicas que son llamadas métodos de carreras evalúa todos los modelos en un subconjunto inicial de remuestreo. En función de sus métricas de rendimiento actuales, algunos conjuntos de parámetros no se consideran en remuestreos posteriores.

Dado un workflow, podemos usar la función workflow_map() para un enfoque de carreras. El paquete finetune contiene funciones para el método de carreras. Calcula un conjunto de métricas de rendimiento (por ejemplo, precisión o RMSE) para un conjunto predefinido de parámetros de ajuste que corresponden a un modelo o receta a través de una o más muestras de los datos.

5.6.1 Optimización ANOVA

Realiza un modelo de análisis de varianza (ANOVA) para probar la significación estadística de las diferentes configuraciones del modelo. Después de evaluar un número inicial de remuestreos, el proceso elimina las combinaciones de parámetros de ajuste que probablemente no sean los mejores resultados usando medidas repetidas de un modelo ANOVA. La función implementada es tune_race_anova

library(finetune)

UseCores <- detectCores() - 1
cluster <- makeCluster(UseCores)
registerDoParallel(cluster)

race_ctrl <- control_race(
  save_pred = TRUE,
  parallel_over = "everything",
  save_workflow = TRUE
  )

tunning_race_anova_results <- workflow_tunning_set_models %>%
  workflow_map(
    "tune_race_anova",
    seed = 1503,
    resamples = ames_folds,
    grid = 100,
    metrics =  metric_set(rmse, mae, mape, rsq),
    control = race_ctrl,
    verbose = TRUE
  )

stopCluster(cluster)

tunning_race_anova_results %>% saveRDS("models/race_anova_results.rds")

Las mismas funciones útiles están disponibles para que este objeto interrogue los resultados y, de hecho, el método básico autoplot() produce tendencias similares:

tunning_race_anova_results %>%
  rank_results(select_best = T) %>%
  select(-c(.config, n, preprocessor, std_err)) %>%
  pivot_wider(names_from = .metric, values_from = mean)

## # A tibble: 15 × 7
##    wflow_id                   model             rank    mae  mape   rmse   rsq
##    <chr>                      <chr>            <int>  <dbl> <dbl>  <dbl> <dbl>
##  1 receta_knn_boost           boost_tree           1 16275.  10.3 25609. 0.898
##  2 receta_knn_rf              rand_forest          2 17676.  11.1 28416. 0.877
##  3 receta_knn_svm_rbf         svm_rbf              3 18390.  11.6 29772. 0.859
##  4 receta_knn_knn             nearest_neighbor     4 19383.  11.5 30727. 0.859
##  5 receta_original_boost      boost_tree           5 20342.  12.4 30962. 0.851
##  6 receta_grande_boost        boost_tree           6 20342.  12.4 30962. 0.851
##  7 receta_original_rf         rand_forest          7 21016.  12.9 33521. 0.830
##  8 receta_grande_rf           rand_forest          8 21016.  12.9 33521. 0.830
##  9 receta_grande_svm_rbf      svm_rbf              9 22677.  13.7 34676. 0.812
## 10 receta_original_svm_rbf    svm_rbf             10 22677.  13.7 34676. 0.812
## 11 receta_grande_knn          nearest_neighbor    11 22584.  13.0 35472. 0.815
## 12 receta_original_knn        nearest_neighbor    12 22584.  13.0 35472. 0.815
## 13 receta_knn_elasticnet      linear_reg          13 24197.  14.7 39883. 0.756
## 14 receta_grande_elasticnet   linear_reg          14 30130.  18.4 44123. 0.694
## 15 receta_original_elasticnet linear_reg          15 30130.  18.4 44123. 0.694

autoplot(
  tunning_race_anova_results,
  rank_metric = "rsq",
  metric = "rsq",
  select_best = TRUE) +
  geom_text(aes(y = mean - 0.10 , label = wflow_id), angle = 90, hjust = 1) +
  lims(y = c(0, 1))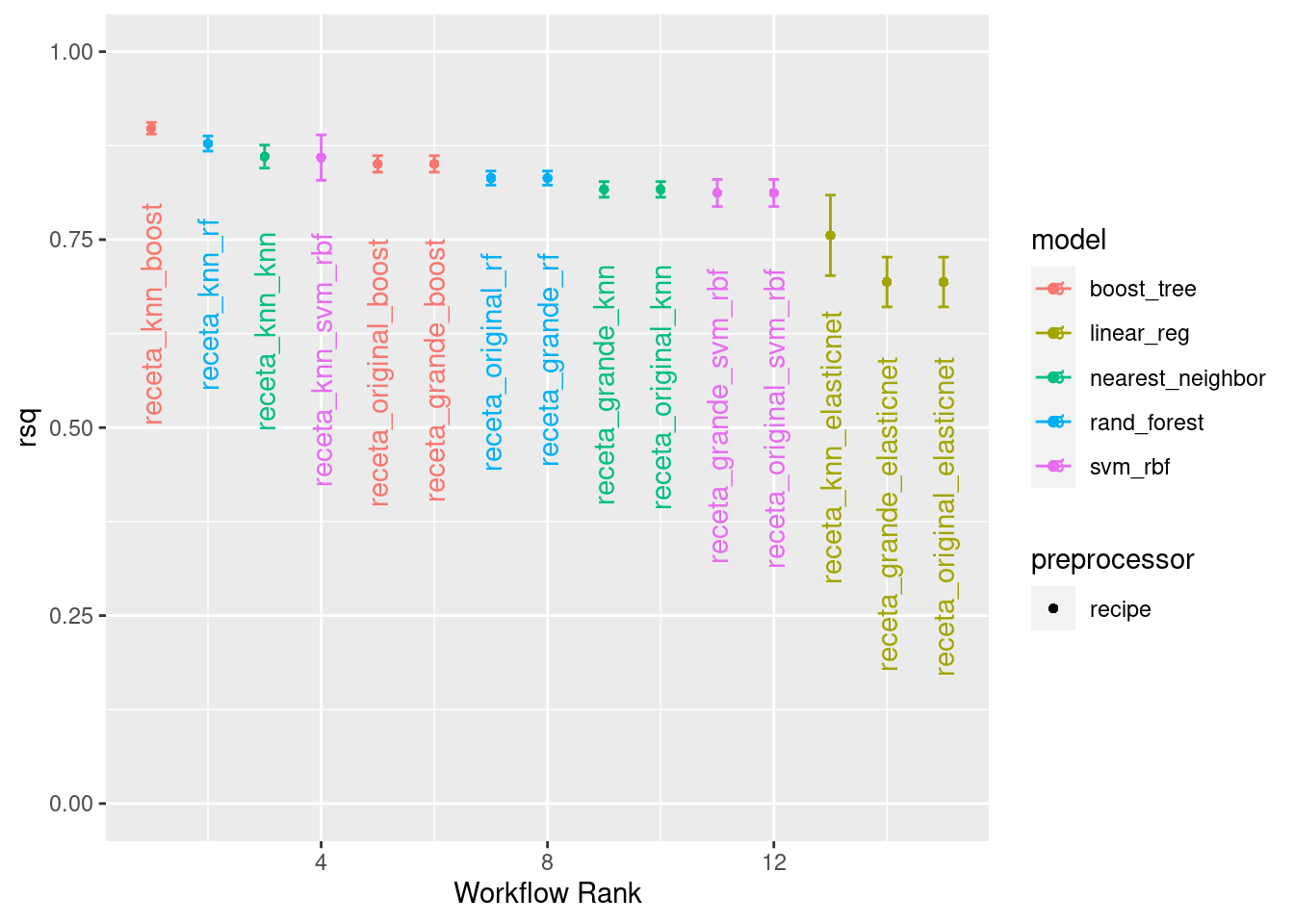

5.6.2 Optimización Logística

Después de evaluar un número inicial de remuestreos, el proceso elimina las combinaciones de parámetros de ajuste que probablemente no sean los mejores resultados usando un modelo estadístico. Para cada combinación por pares de parámetros de ajuste, se calculan las estadísticas de ganancia/pérdida y se usa un modelo de regresión logística para medir la probabilidad de que cada combinación gane en general. Esto se logra mediante la función tune_race_win_loss

UseCores <- detectCores() - 1
cluster <- makeCluster(UseCores)
registerDoParallel(cluster)

race_ctrl <- control_race(
  save_pred = TRUE,
  parallel_over = "everything",
  save_workflow = TRUE
  )

tunning_race_win_loss_results <- workflow_tunning_set_models %>%
  workflow_map(
    "tune_race_win_loss",
    seed = 1503,
    resamples = ames_folds,
    grid = 100,
    metrics =  metric_set(rmse, mae, mape, rsq),
    control = race_ctrl,
    verbose = TRUE
  )

stopCluster(cluster)

tunning_race_win_loss_results %>% saveRDS("models/race_win_loss_results.rds")

Las mismas funciones útiles están disponibles para que este objeto interrogue los resultados y, de hecho, el método básico autoplot() produce tendencias similares:

tunning_race_win_loss_results %>%
  rank_results(select_best = T) %>%
  select(-c(.config, n, preprocessor, std_err)) %>%
  pivot_wider(names_from = .metric, values_from = mean)

## # A tibble: 15 × 7
##    wflow_id                   model             rank    mae  mape   rmse   rsq
##    <chr>                      <chr>            <int>  <dbl> <dbl>  <dbl> <dbl>
##  1 receta_knn_boost           boost_tree           1 16216.  10.2 25608. 0.898
##  2 receta_knn_rf              rand_forest          2 17637.  11.1 28341. 0.878
##  3 receta_knn_svm_rbf         svm_rbf              3 18390.  11.6 29772. 0.859
##  4 receta_knn_knn             nearest_neighbor     4 19383.  11.5 30727. 0.859
##  5 receta_original_boost      boost_tree           5 20583.  12.5 31149. 0.850
##  6 receta_grande_boost        boost_tree           6 20583.  12.5 31149. 0.850
##  7 receta_original_rf         rand_forest          7 21012.  12.9 33503. 0.830
##  8 receta_grande_rf           rand_forest          8 21012.  12.9 33503. 0.830
##  9 receta_grande_svm_rbf      svm_rbf              9 22677.  13.7 34676. 0.812
## 10 receta_original_svm_rbf    svm_rbf             10 22677.  13.7 34676. 0.812
## 11 receta_grande_knn          nearest_neighbor    11 22584.  13.0 35472. 0.815
## 12 receta_original_knn        nearest_neighbor    12 22584.  13.0 35472. 0.815
## 13 receta_knn_elasticnet      linear_reg          13 24197.  14.7 39883. 0.756
## 14 receta_grande_elasticnet   linear_reg          14 30130.  18.4 44123. 0.694
## 15 receta_original_elasticnet linear_reg          15 30130.  18.4 44123. 0.694

autoplot(
  tunning_race_win_loss_results,
  rank_metric = "rsq",
  metric = "rsq",
  select_best = TRUE) +
  geom_text(aes(y = mean - 0.10 , label = wflow_id), angle = 90, hjust = 1) +
  lims(y = c(0, 1))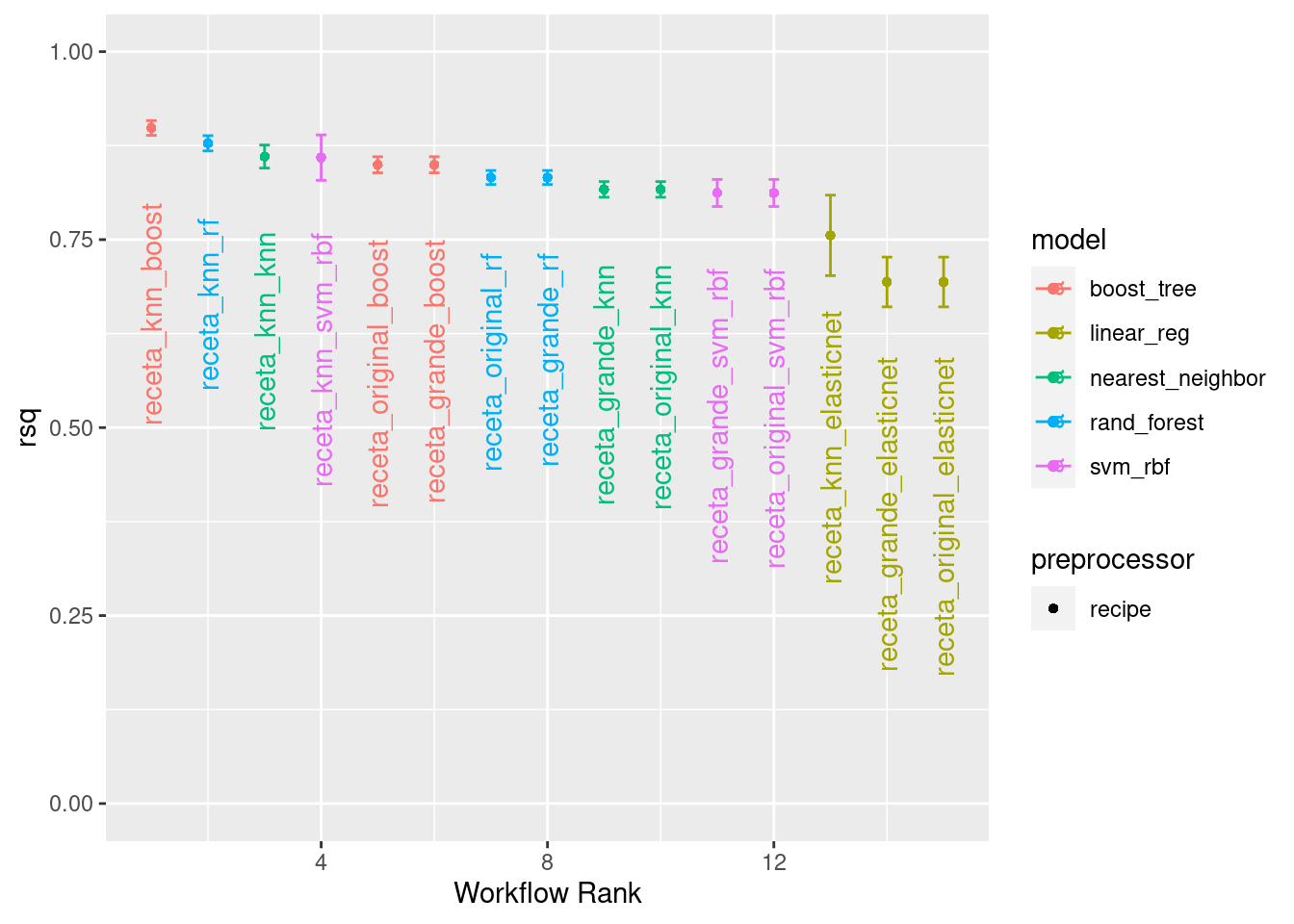

5.6.3 Optimización Bayesiana

La función tune_bayes usa modelos para crear nuevas combinaciones de hiperparámetros que sean candidatos de tunning basado en resultados previos.

El método utiliza métodos MCMC de simulación bayesiana para determinar los hiperparámetros óptimos. A partir de un buen candidato se realiza una exploración aleatoria que permita encontrar nuevos óptimos o sub-óptimos a encontrar. Es posible configurar el número de iteraciones antes regresar al último óptimo o sub-óptimo para continuar la exploración por otro lado.

La forma de implementarlo es muy similar a las técnicas anteriores. Esta vez se utiliza la función tune_bayes y control_bayes.

UseCores <- detectCores() - 1
cluster <- makeCluster(UseCores)
registerDoParallel(cluster)

race_ctrl <- control_bayes(
  verbose = TRUE,
  save_pred = TRUE,
  parallel_over = "everything",
  save_workflow = TRUE
  )

set.seed(20220603)
tunning_race_bayes_results <- workflow_tunning_set_models %>%
  workflow_map(
    "tune_bayes",
    seed = 1503,
    resamples = ames_folds,
    iter = 100,
    metrics =  metric_set(rmse, mae, mape, rsq),
    control = race_ctrl,
    verbose = TRUE
  )

stopCluster(cluster)

tunning_race_bayes_results %>% saveRDS("models/race_bayes_results.rds")

tunning_race_bayes_results <- readRDS("models/race_bayes_results.rds")

Las mismas funciones útiles están disponibles para que este objeto interrogue los resultados y, de hecho, el método básico autoplot() produce tendencias similares:

tunning_race_bayes_results %>%
  filter(stringr::str_detect(wflow_id, pattern = "(rf)|(boost)", negate = T) ) %>% 
  rank_results(select_best = T) %>%
  select(-c(.config, n, preprocessor, std_err)) %>%
  pivot_wider(names_from = .metric, values_from = mean)

## # A tibble: 9 × 7
##   wflow_id                   model             rank    mae  mape   rmse   rsq
##   <chr>                      <chr>            <int>  <dbl> <dbl>  <dbl> <dbl>
## 1 receta_knn_svm_rbf         svm_rbf              1 17912.  11.4 28954. 0.867
## 2 receta_knn_knn             nearest_neighbor     2 19465.  11.6 30463. 0.861
## 3 receta_original_svm_rbf    svm_rbf              3 22651.  13.7 34736. 0.811
## 4 receta_grande_svm_rbf      svm_rbf              4 22651.  13.7 34736. 0.811
## 5 receta_original_knn        nearest_neighbor     5 22512.  13.0 35283. 0.818
## 6 receta_grande_knn          nearest_neighbor     6 22512.  13.0 35283. 0.818
## 7 receta_knn_elasticnet      linear_reg           7 24197.  14.7 39880. 0.756
## 8 receta_original_elasticnet linear_reg           8 30129.  18.4 44122. 0.694
## 9 receta_grande_elasticnet   linear_reg           9 30129.  18.4 44122. 0.694

tunning_race_bayes_results %>% 
  filter(stringr::str_detect(wflow_id, pattern = "(rf)|(boost)", negate = T) ) %>% 
  autoplot(
    rank_metric = "rsq",
    metric = "rsq",
    select_best = TRUE) +
    geom_text(aes(y = mean - 0.10 , label = wflow_id), angle = 90, hjust = 1) +
    lims(y = c(0, 1))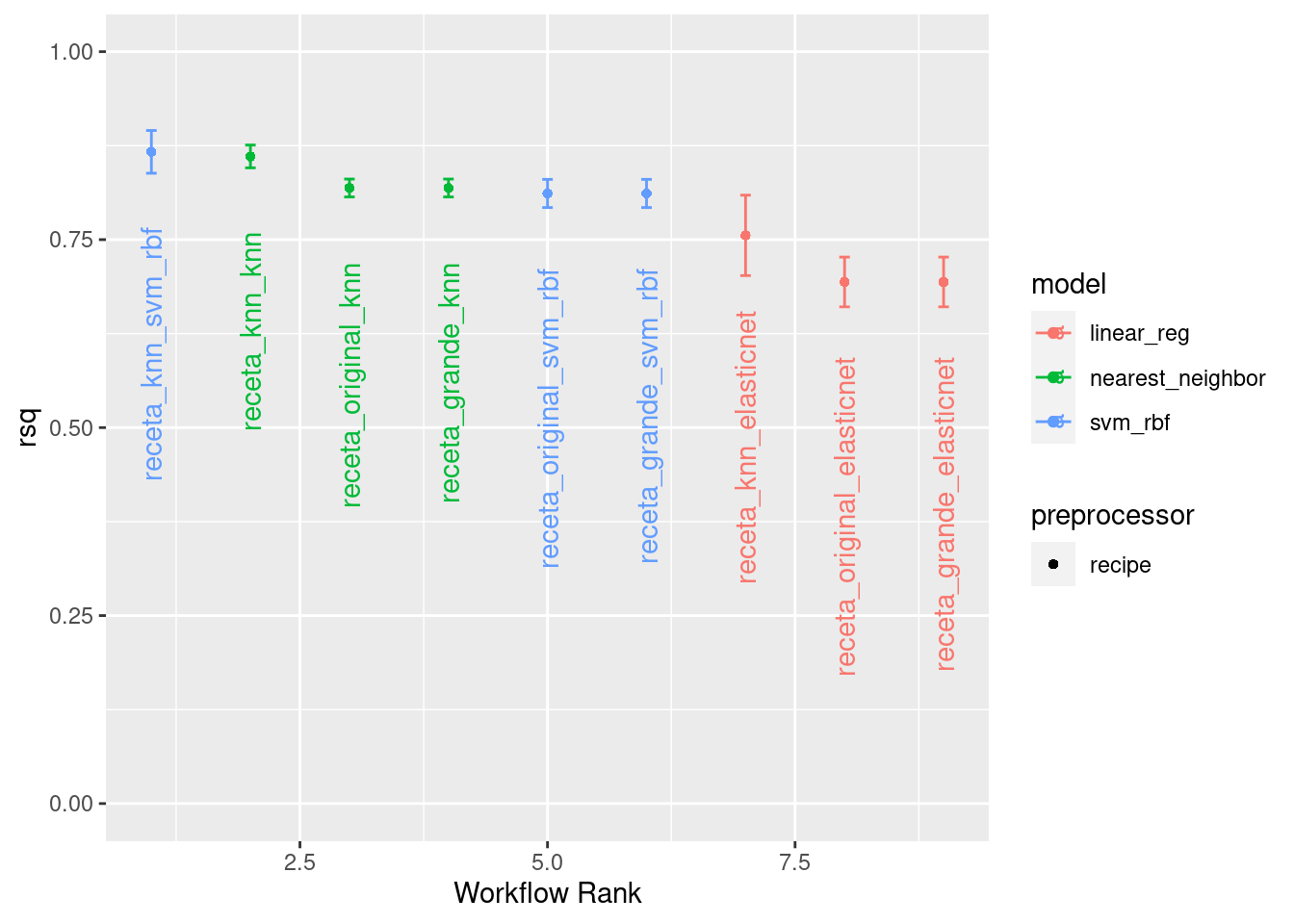

5.7 Stacking

El ensamblaje de modelos es un proceso en el que se utilizan varios modelos base para predecir un resultado.

La motivación para usar modelos de conjunto es reducir el error de generalización de la predicción.
Siempre que los modelos base sean diversos e independientes, el error de predicción disminuye cuando se utiliza el enfoque de conjunto.
Aunque el modelo de conjunto tiene varios modelos base dentro del modelo, actúa y funciona como un solo modelo.

Un conjunto de modelos, donde las predicciones de varios modelos individuales se agregan para hacer una predicción, puede producir un modelo final de alto rendimiento.

Los métodos más populares para crear modelos de conjuntos son:

Bagging
Bosques aleatorios
Boosting

Cada uno de estos métodos combina las predicciones de múltiples versiones del mismo tipo de modelo. Uno de los primeros métodos para crear conjuntos es el apilamiento de modelos (stacking).

Stacking combina las predicciones de múltiples modelos de cualquier tipo.

Por ejemplo, una regresión logística, un árbol de clasificación y una máquina de vectores de soporte se pueden incluir en un conjunto de apilamiento, así como diferentes configuraciones de un mismo modelo.

El proceso de construcción de un conjunto apilado es:

Reunir el conjunto de entrenamiento de predicciones (producidas mediante remuestreo).
Crear un modelo para combinar estas predicciones.
Para cada modelo del conjunto, ajustar el modelo en el conjunto de entrenamiento original.

5.7.1 Elección de modelos

Para cada observación en el conjunto de entrenamiento, el apilamiento (stacking) requiere una predicción fuera de la muestra de algún tipo.

Para comenzar a ensamblar con el paquete stacks, se crea una pila de datos vacía usando la función stacks() y luego se agrega el flujo de trabajo para ajustar una amplia variedad de modelos a estos datos.

library(tidymodels)
library(stacks)
tidymodels_prefer()

concrete_stack <- stacks() %>% 
  add_candidates(tunning_models_result)

concrete_stack

## # A data stack with 15 model definitions and 996 candidate members:
## #   receta_original_elasticnet: 100 model configurations
## #   receta_original_knn: 100 model configurations
## #   receta_original_rf: 97 model configurations
## #   receta_original_svm_rbf: 100 model configurations
## #   receta_original_boost: 100 model configurations
## #   receta_knn_elasticnet: 100 model configurations
## #   receta_knn_knn: 100 model configurations
## #   receta_knn_rf: 99 model configurations
## #   receta_knn_svm_rbf: 100 model configurations
## #   receta_knn_boost: 100 model configurations
## #   receta_grande_elasticnet: 0 model configurations
## #   receta_grande_knn: 0 model configurations
## #   receta_grande_rf: 0 model configurations
## #   receta_grande_svm_rbf: 0 model configurations
## #   receta_grande_boost: 0 model configurations
## # Outcome: Sale_Price (integer)

La regularización mediante la penalización de lazo tiene varias ventajas:

El uso de la penalización de lazo puede eliminar modelos (y, a veces, tipos de modelos completos) del conjunto.
La correlación entre los candidatos del conjunto tiende a ser muy alta y la regularización ayuda a mitigar este problema.

Dado que nuestro resultado es numérico, se utiliza la regresión lineal para el metamodelo.

set.seed(20220612)

assembly <- concrete_stack %>% 
  blend_predictions(metric = metric_set(rmse, mae, mape, rsq))

assembly %>% saveRDS("models/stack_predictions.rds")

assembly <- readRDS("models/stack_predictions.rds")

assembly

## ── A stacked ensemble model ─────────────────────────────────────
## 
## Out of 996 possible candidate members, the ensemble retained 19.
## Penalty: 0.1.
## Mixture: 1.
## 
## The 10 highest weighted members are:

## # A tibble: 10 × 3
##    member                      type             weight
##    <chr>                       <chr>             <dbl>
##  1 receta_knn_svm_rbf_1_007    svm_rbf          0.504 
##  2 receta_knn_boost_1_058      boost_tree       0.316 
##  3 receta_knn_boost_1_086      boost_tree       0.0962
##  4 receta_knn_boost_1_041      boost_tree       0.0925
##  5 receta_knn_boost_1_040      boost_tree       0.0907
##  6 receta_knn_boost_1_035      boost_tree       0.0843
##  7 receta_knn_boost_1_025      boost_tree       0.0739
##  8 receta_original_knn_1_003   nearest_neighbor 0.0600
##  9 receta_knn_svm_rbf_1_100    svm_rbf          0.0483
## 10 receta_original_boost_1_002 boost_tree       0.0432

## 
## Members have not yet been fitted with `fit_members()`.

autoplot(assembly, "weights") + 
  theme_minimal()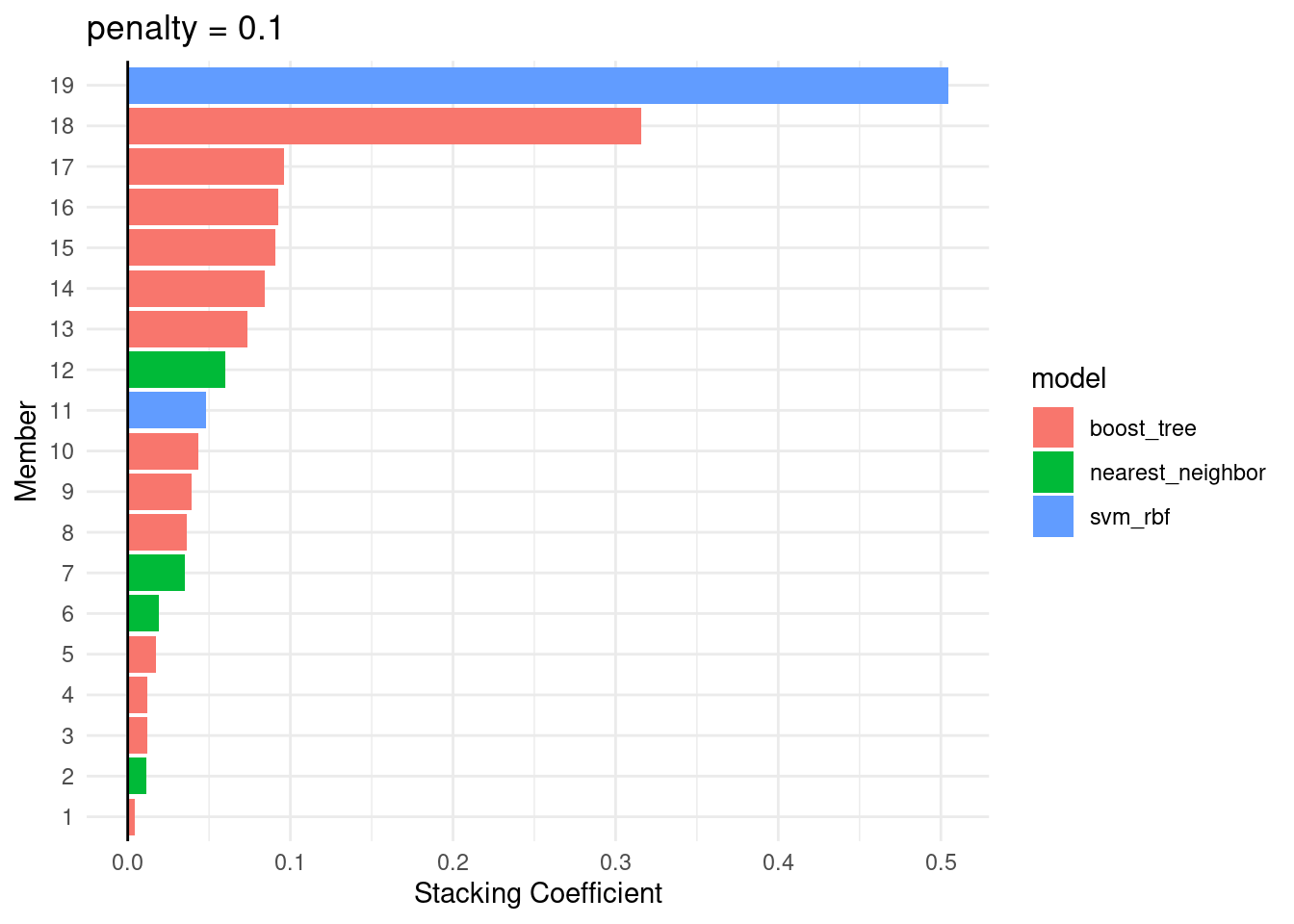

Esto evalúa el modelo de meta aprendizaje sobre un grid predefinido de valores de penalización de lazo y utiliza un método de remuestreo interno para determinar el mejor valor.

El método autoplot() nos ayuda a comprender si el método de penalización predeterminado fue suficiente:

autoplot(assembly)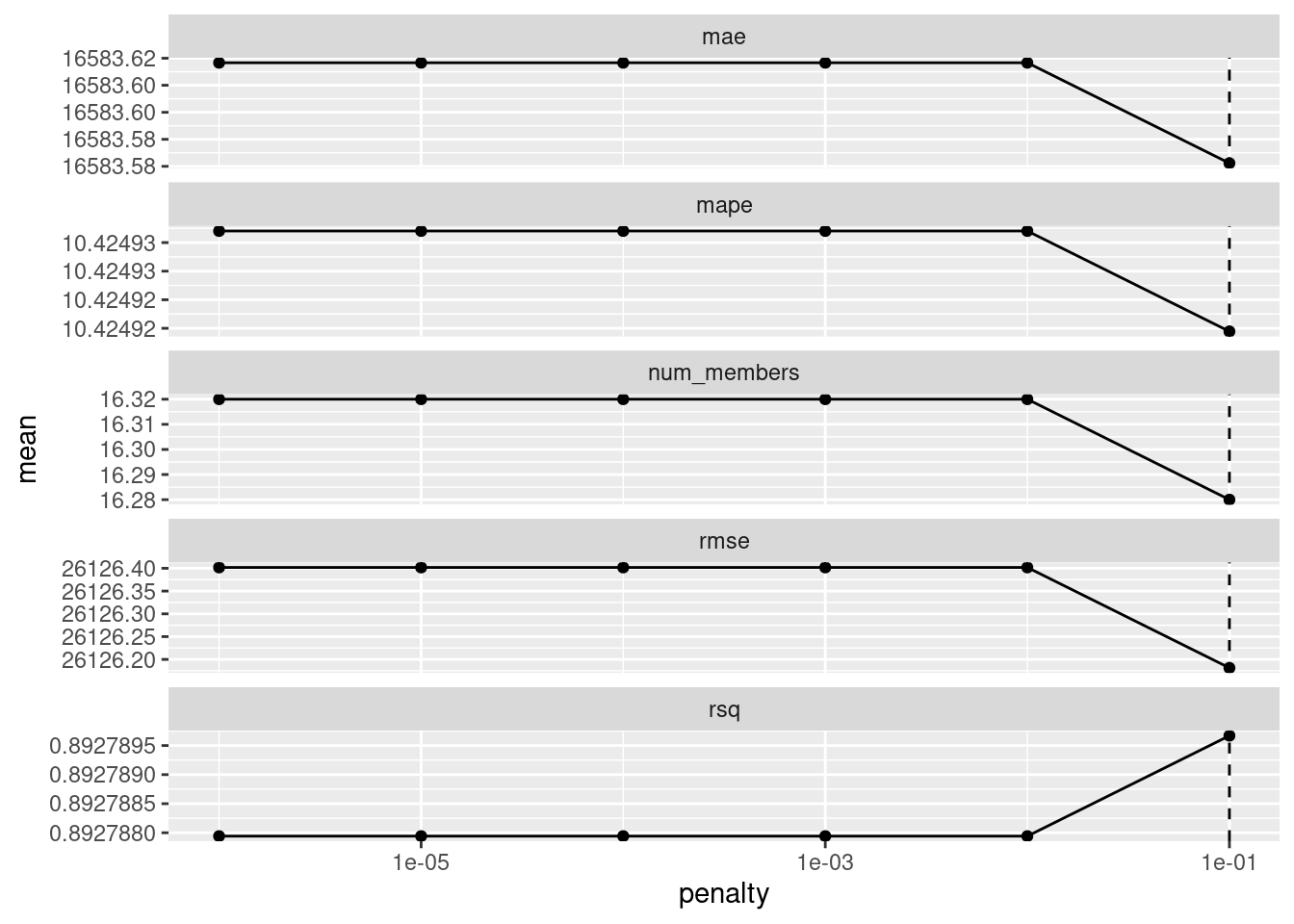

El panel de en medio muestra el número promedio de modelos del conjunto retenidos por el modelo de meta aprendizaje.

Es posible que el rango predeterminado no nos haya servido bien aquí. Para evaluar el modelo de meta aprendizaje con penalizaciones mayores.

set.seed(20220612)

assembly_v2 <- concrete_stack %>% 
  blend_predictions(
    metric = metric_set(rmse, mae, mape, rsq),
    penalty = 10^seq(-5, 5, length = 50)
  )

assembly_v2 %>% saveRDS("models/stack_predictions_v2.rds")

assembly_v2 <- readRDS("models/stack_predictions_v2.rds")

autoplot(assembly_v2)

## Warning: Removed 1 rows containing missing values (geom_point).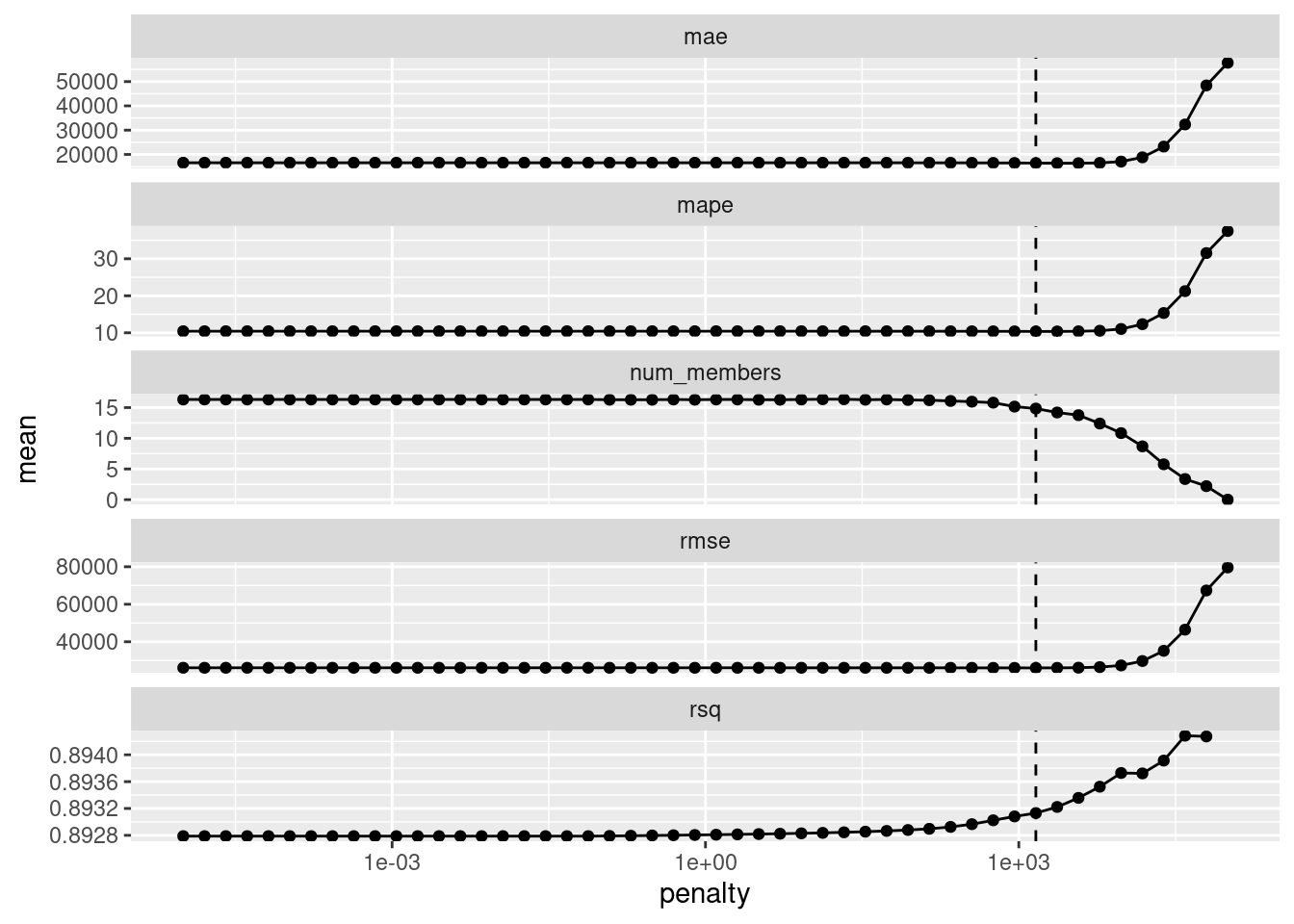

El valor de penalización asociado a las curvas fue de 1456.34. La impresión del objeto muestra los detalles del modelo de meta aprendizaje:

assembly_v2

## ── A stacked ensemble model ─────────────────────────────────────
## 
## Out of 996 possible candidate members, the ensemble retained 16.
## Penalty: 1456.34847750124.
## Mixture: 1.
## 
## The 10 highest weighted members are:

## # A tibble: 10 × 3
##    member                      type             weight
##    <chr>                       <chr>             <dbl>
##  1 receta_knn_boost_1_058      boost_tree       0.338 
##  2 receta_knn_boost_1_086      boost_tree       0.102 
##  3 receta_knn_boost_1_040      boost_tree       0.0981
##  4 receta_knn_boost_1_035      boost_tree       0.0938
##  5 receta_knn_boost_1_041      boost_tree       0.0829
##  6 receta_knn_boost_1_025      boost_tree       0.0665
##  7 receta_original_knn_1_003   nearest_neighbor 0.0516
##  8 receta_original_boost_1_002 boost_tree       0.0427
##  9 receta_knn_knn_1_004        nearest_neighbor 0.0388
## 10 receta_knn_boost_1_047      boost_tree       0.0320

## 
## Members have not yet been fitted with `fit_members()`.

El modelo de meta aprendizaje contenía cuatro coeficientes de combinación. El método autoplot() se puede usar nuevamente para mostrar las contribuciones de cada tipo de modelo:

autoplot(assembly_v2, "weights") + 
  theme_minimal()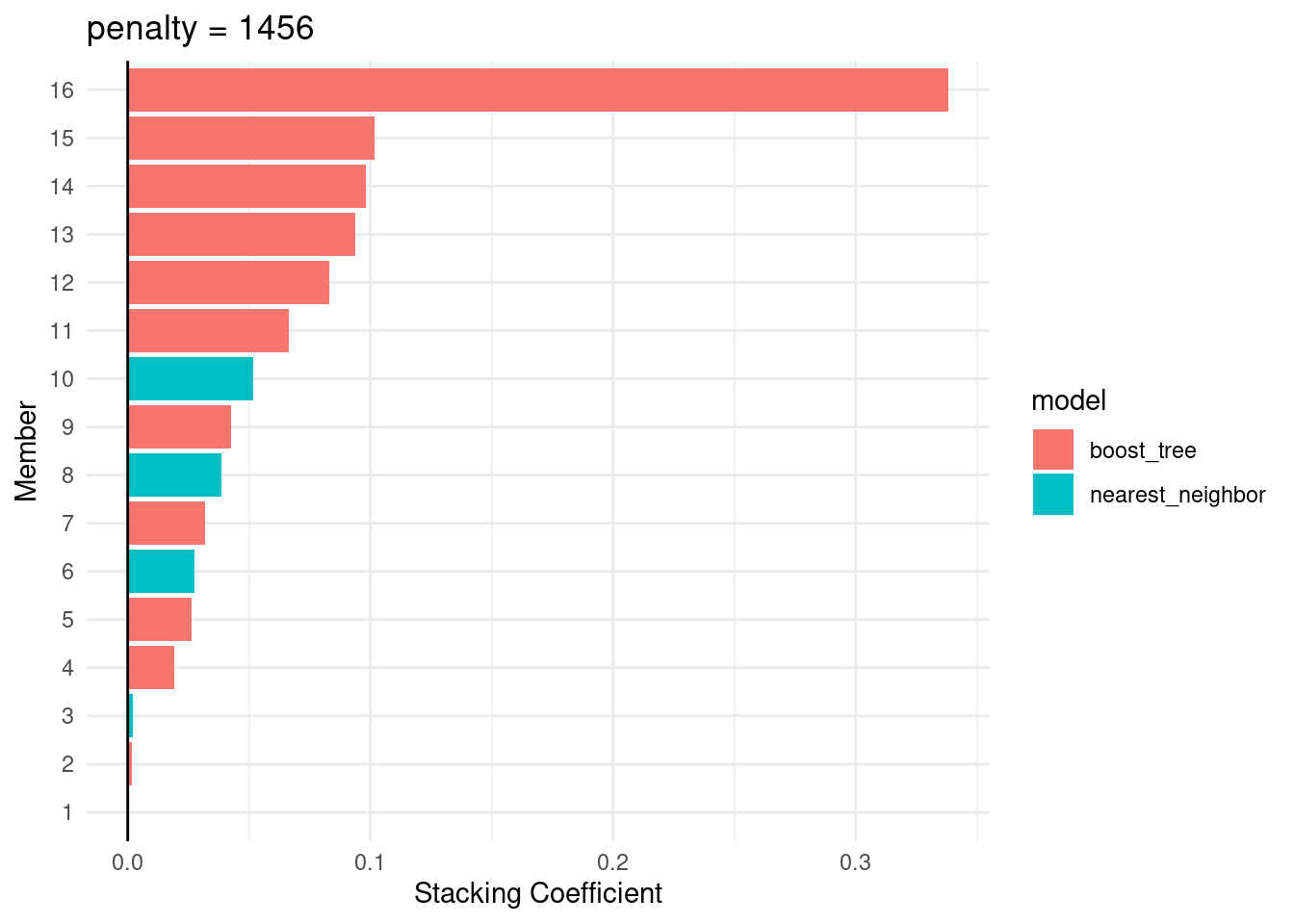

El modelo de bosques aleatorios tiene la mayor contribución al conjunto. Para este conjunto, el resultado se predice con la ecuación:

\[\begin{aligned} \text{Predicción ensamblada} = -3130.71 &+ 0.0516 * \text{receta_original_knn_1_003} \\ &+ 0.0427 * \text{receta_original_boost_1_002} \\ &+ 0.0015 * \text{receta_original_boost_1_075} \\ &+ 0.0274 * \text{receta_knn_knn_1_003} \\ &+ 0.0020 * \text{receta_knn_knn_1_053} \\ &+ 0.0387 * \text{receta_knn_knn_1_004} \\ &+ 0.3380 * \text{receta_knn_boost_1_058} \\ &+ 0.0192 * \text{receta_knn_boost_1_028} \\ &+ 0.0980 * \text{receta_knn_boost_1_040} \\ &+ 0.0264 * \text{receta_knn_boost_1_013} \\ &+ 0.0938 * \text{receta_knn_boost_1_035} \\ &+ 0.0319 * \text{receta_knn_boost_1_047} \\ &+ 0.0664 * \text{receta_knn_boost_1_025} \\ &+ 0.1015 * \text{receta_knn_boost_1_086} \\ &+ 0.0006 * \text{receta_knn_boost_1_045} \\ &+ 0.0829 * \text{receta_knn_boost_1_041} \\ \end{aligned}\]

Ahora sabemos cómo se pueden combinar sus predicciones en una predicción final para el conjunto. Sin embargo, estos ajustes de modelos individuales aún no se han creado.

5.7.2 Ajuste final

Para poder usar el modelo de stacking, se requieren los ajustes de todos los modelos candidatos. Estos utilizan todo el conjunto de entrenamiento con los predictores originales.

fit_assembly <- fit_members(assembly_v2)

fit_assembly %>%  saveRDS("models/stack_fit_members.rds")

fit_assembly <- readRDS("models/stack_fit_members.rds")

fit_assembly

## ── A stacked ensemble model ─────────────────────────────────────
## 
## Out of 996 possible candidate members, the ensemble retained 16.
## Penalty: 1456.34847750124.
## Mixture: 1.
## 
## The 10 highest weighted members are:

## # A tibble: 10 × 3
##    member                      type             weight
##    <chr>                       <chr>             <dbl>
##  1 receta_knn_boost_1_058      boost_tree       0.338 
##  2 receta_knn_boost_1_086      boost_tree       0.102 
##  3 receta_knn_boost_1_040      boost_tree       0.0981
##  4 receta_knn_boost_1_035      boost_tree       0.0938
##  5 receta_knn_boost_1_041      boost_tree       0.0829
##  6 receta_knn_boost_1_025      boost_tree       0.0665
##  7 receta_original_knn_1_003   nearest_neighbor 0.0516
##  8 receta_original_boost_1_002 boost_tree       0.0427
##  9 receta_knn_knn_1_004        nearest_neighbor 0.0388
## 10 receta_knn_boost_1_047      boost_tree       0.0320

Esto actualiza el objeto de apilamiento con los objetos de flujo de trabajo ajustados para cada miembro. En este punto, el modelo de stacking se puede utilizar para la predicción.

regression_metrics <- metric_set(rmse, mae, mape, rsq, ccc)

fit_assembly_pred_test <- predict(fit_assembly, ames_test) %>% 
  bind_cols(ames_test)

fit_assembly_pred_test %>% regression_metrics(Sale_Price, .pred)

## # A tibble: 5 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard   25774.   
## 2 mae     standard   16377.   
## 3 mape    standard      10.2  
## 4 rsq     standard       0.898
## 5 ccc     standard       0.944

5.7.3 Comparación de métricas

Para ver la efectividad del ensamblaje, realizamos una comparación con el mejor modelo entrenado anteriormente (XGBoost). Es importante que la comparación se realice utilizando los mismos datos de prueba.

multi_metric(results, truth = Sale_Price, estimate = pred_xgb_reg)

## # A tibble: 5 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard   26851.   
## 2 rsq     standard       0.889
## 3 mae     standard   17078.   
## 4 mape    standard      10.5  
## 5 ccc     standard       0.939

Este capítulo demuestra cómo combinar diferentes modelos en un conjunto para un mejor desempeño predictivo. El proceso de creación del conjunto puede eliminar automáticamente los modelos candidatos para encontrar un pequeño subconjunto que mejore el rendimiento.

5.8 Ejercicios

Para obtener un mejor aprendizaje de este capítulo, cada alumno deberá:

Replicar este proceso eligiendo un número de iteraciones mayor a 500 con cualquiera de las metodologías revisadas en este capítulo.
Realizar el proceso análogo con los datos de respuesta categórica y mandar un reporte con sus resultados