Capítulo 9 Clustering No Jerárquico
9.1 Cálculo de distancia
Otro parámetro que podemos ajustar para el modelo es la distancia usada, existen diferentes formas de medir qué tan “cerca” están dos puntos entre sí, y las diferencias entre estos métodos pueden volverse significativas en dimensiones superiores.
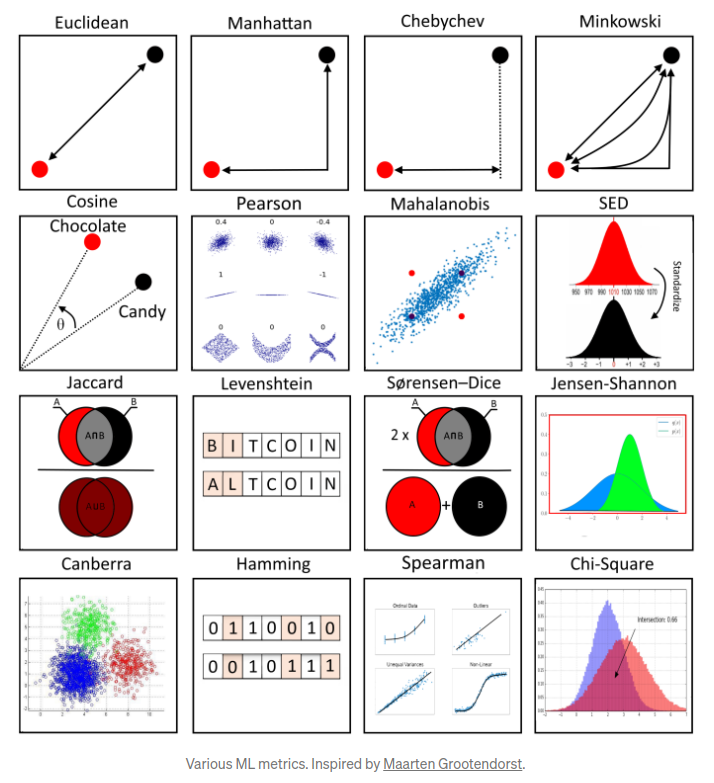
- La más utilizada es la distancia euclidiana, el tipo estándar de distancia.
\[d(X,Y) = \sqrt{\sum_{i=1}^{n} (x_i-y_i)^2}\]
- Otra métrica es la llamada distancia de Manhattan, que mide la distancia tomada en cada dirección cardinal, en lugar de a lo largo de la diagonal.
\[d(X,Y) = \sum_{i=1}^{n} |x_i - y_i|\]
- De manera más general, las anteriores son casos particulares de la distancia de Minkowski, cuya fórmula es:
\[d(X,Y) = (\sum_{i=1}^{n} |x_i-y_i|^p)^{\frac{1}{p}}\]
- La distancia de coseno es ampliamente en análisis de texto, sistemas de recomendación.
\[d(X,Y)= 1 - \frac{\sum_{i=1}^{n}{X_iY_i}}{\sqrt{\sum_{i=1}^{n}{X_i^2}}\sqrt{\sum_{i=1}^{n}{Y_i^2}}}\]
- La distancia de Jaccard es ampliamente usada para medir similitud cuando se trata de variables categóricas. Es usado en análisis de texto y sistemas de recomendación.
\[d(X, Y) = \frac{X \cap Y}{X \cup Y}\]
- La distancia de Gower´s mide la similitud entre variables de forma distinta dependiendo del tipo de dato (numérica, nominal, ordinal).
\[D_{Gower}(X_1, X_2) = 1 - \frac{1}{p} \sum_{j=1}^{p}{s_j(X_1, X_2)} ; \quad \quad s_j(X_1, X_2)=1-\frac{|y_{1j}-y_{2j}|}{R_j} \] Para mayor detalle sobre el funcionamiento de la métrica, revisar el siguiente link
9.1.1 Distancias homogéneas
Las distancias basadas en la correlación son ampliamente usadas en múltiples análisis. La función get_dist() puede ser usada para calcular la distancia basada en correlación. Esta medida puede calcularse mediante pearson, spearman o kendall.
library(factoextra)
USArrests_scaled <- scale(USArrests)
dist.cor <- get_dist(USArrests_scaled, method = "pearson")
round(as.matrix(dist.cor)[1:7, 1:7], 1)## Alabama Alaska Arizona Arkansas California Colorado Connecticut
## Alabama 0.0 0.7 1.4 0.1 1.9 1.7 1.7
## Alaska 0.7 0.0 0.8 0.4 0.8 0.5 1.9
## Arizona 1.4 0.8 0.0 1.2 0.3 0.6 0.8
## Arkansas 0.1 0.4 1.2 0.0 1.6 1.4 1.9
## California 1.9 0.8 0.3 1.6 0.0 0.1 0.7
## Colorado 1.7 0.5 0.6 1.4 0.1 0.0 1.0
## Connecticut 1.7 1.9 0.8 1.9 0.7 1.0 0.09.1.2 Distancias mixtas
La naturaleza los datos es muy distinta. Existen datos numéricos, nominales y ordinales que requieren de un procesamiento distinto. Es de particular interés analizar la distancia entre observaciones cuando se trata de variables con diferente naturaleza:
numérico - numérico
numérico - nominal
numérico - ordinal
nominal - nominal
nominal - ordinal
Existe una función en R que detecta la naturaleza de cada variable y calcula la asociación entre individuos.
library(cluster)
library(dplyr)
data(flower)
glimpse(flower)## Rows: 18
## Columns: 8
## $ V1 <fct> 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0
## $ V2 <fct> 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0
## $ V3 <fct> 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1
## $ V4 <fct> 4, 2, 3, 4, 5, 4, 4, 2, 3, 5, 5, 1, 1, 4, 3, 4, 2, 2
## $ V5 <ord> 3, 1, 3, 2, 2, 3, 3, 2, 1, 2, 3, 2, 2, 2, 2, 2, 2, 1
## $ V6 <ord> 15, 3, 1, 16, 2, 12, 13, 7, 4, 14, 8, 9, 6, 11, 10, 18, 17, 5
## $ V7 <dbl> 25, 150, 150, 125, 20, 50, 40, 100, 25, 100, 45, 90, 20, 80, 40, 20…
## $ V8 <dbl> 15, 50, 50, 50, 15, 40, 20, 15, 15, 60, 10, 25, 10, 30, 20, 60, 60,…Como puede observarse, cada una de las variables anteriores tiene una naturaleza distinta. La función daisy() calcula la matriz de disimilaridades de acuerdo con la metodología correspondiente a cada par de variables.
dd <- daisy(flower)
round(as.matrix(dd)[1:10, 1:10], 2)## 1 2 3 4 5 6 7 8 9 10
## 1 0.00 0.89 0.53 0.35 0.41 0.23 0.29 0.42 0.58 0.61
## 2 0.89 0.00 0.51 0.55 0.62 0.66 0.60 0.46 0.43 0.45
## 3 0.53 0.51 0.00 0.57 0.37 0.30 0.49 0.60 0.45 0.47
## 4 0.35 0.55 0.57 0.00 0.64 0.42 0.34 0.30 0.81 0.56
## 5 0.41 0.62 0.37 0.64 0.00 0.34 0.42 0.47 0.33 0.38
## 6 0.23 0.66 0.30 0.42 0.34 0.00 0.19 0.57 0.51 0.41
## 7 0.29 0.60 0.49 0.34 0.42 0.19 0.00 0.41 0.59 0.59
## 8 0.42 0.46 0.60 0.30 0.47 0.57 0.41 0.00 0.64 0.66
## 9 0.58 0.43 0.45 0.81 0.33 0.51 0.59 0.64 0.00 0.43
## 10 0.61 0.45 0.47 0.56 0.38 0.41 0.59 0.66 0.43 0.009.1.3 Visualización de distancias
En cualquier análisis, es de gran valor contar con un gráfico que permita conocer de manera práctica y simple el resumen de distancias. Un mapa de calor es una solución bastante útil, el cual representará de en una escala de color a los elementos cerca y lejos.
fviz_dist(dist.cor)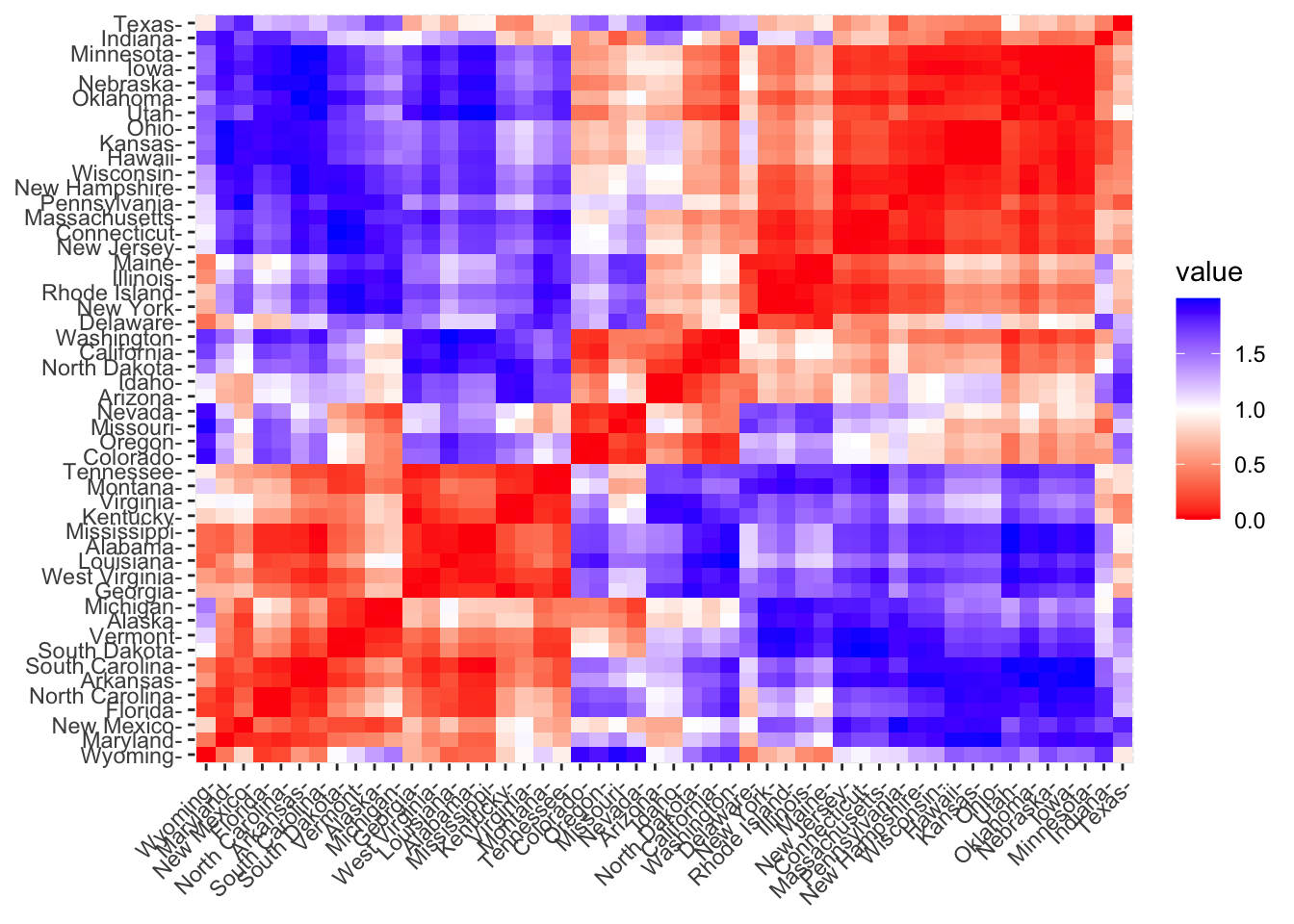
El nivel del color es proporcional al valor de disimilaridad entre observaciones. Cuando la distancia es cero, el color es rojo puro y cuando la distancia es amplia, el color es azul puro. Los elementos que pertenecen a un mismo cluster se muestran en orden consecutivo.
9.2 Tendencia de factibilidad
Este análisis es considerado como la evaluación de factibilidad de implementar análisis de clustering. Antes de aplicar cualquier técnica de clustering vale la pena evaluar si el conjunto de datos contiene clusters naturales significativos (i.e. estructuras no aleatorias) o no. En caso de que sí existan estructuras conglomeradas naturales, se deberá proceder a identificar el número de clusters a extraer.

A diferencia de otros tipos de análisis, una desventaja que tiene el análisis de clustering es que en todo momento regresarán clusters incluso cuando los datos no contengan tal estructura, por lo que si ciegamente se implementa un método de clustering, este dividirá los datos en clusters debido a que es lo esperado a realizar. las librerías usadas en R serán factoextra y hopkins.
head(iris, 5)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosadf <- iris %>% select_if(is.numeric)
random_df <- df %>%
apply(2, function(x){runif(length(x), min(x), max(x))}) %>%
as_tibble()
df_scaled <- scale(df)
random_df_scaled <- scale(random_df)Se comienza con una evaluación visual sobre los datos para evaluar la significancia de los clusters. Debido a que los más probable es que los datos tengan más de dos dimensiones, se aprovecha el análisis de componentes principales para representar los datos en un espacio de dimensión menor.
library(patchwork)
iris_plot <- fviz_pca_ind(
prcomp(df_scaled), title = "PCA - Iris data",
geom = "point", ggtheme = theme_classic(),
legend = "bottom"
)
random_plot <- fviz_pca_ind(
prcomp(random_df_scaled), title = "PCA - Random data",
geom = "point", ggtheme = theme_classic(),
legend = "bottom"
)
iris_plot + random_plot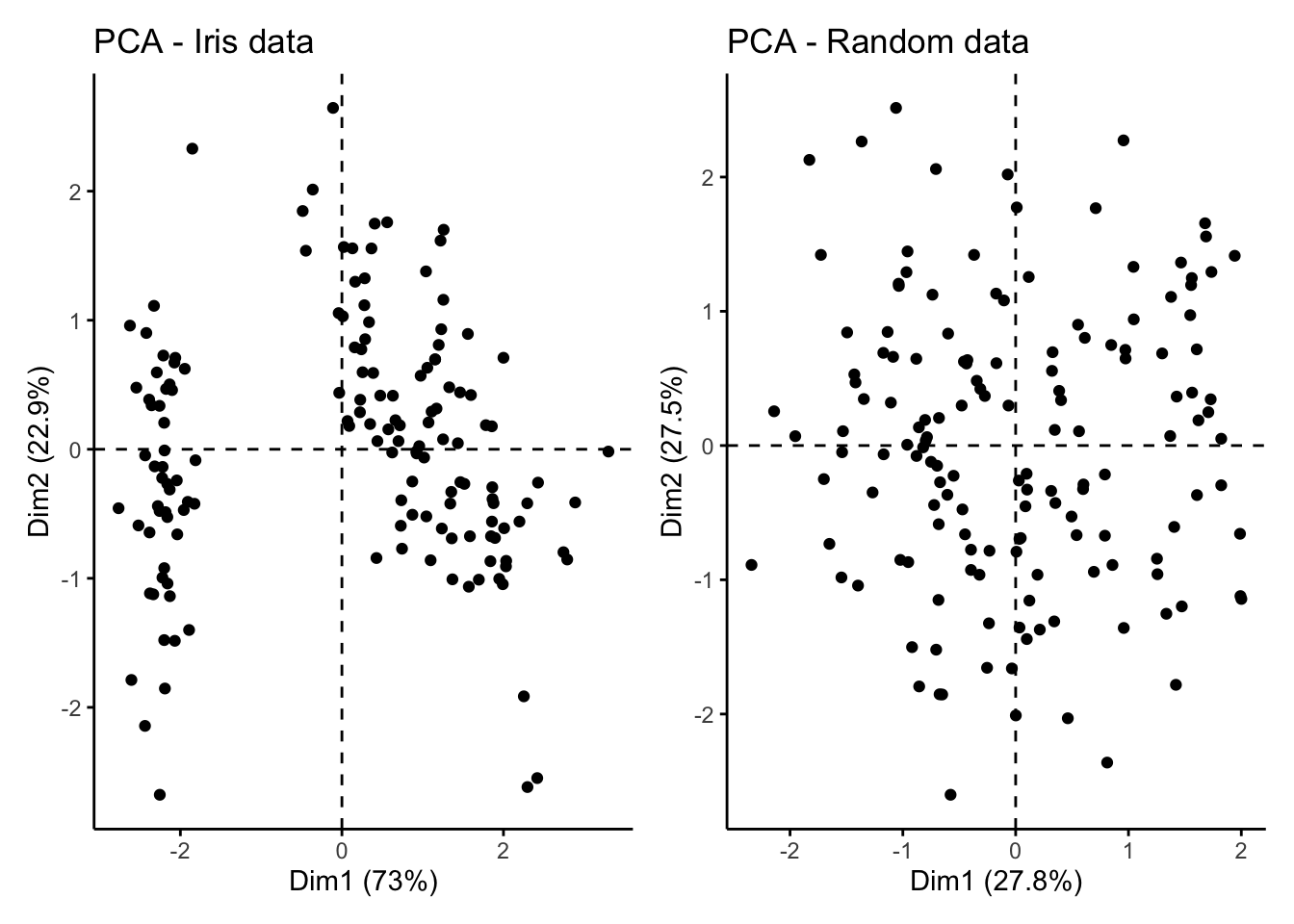
Puede observarse en el primer gráfico que, al menos existen 2 clusters significativos, con posibilidad de que sean 3. A diferencia del gráfico de la derecha que no muestra una tendencia en la estructura conglomerativa.
Es sumamente importante realizar esta evaluación porque
set.seed(12853)
km_res2 <- kmeans(random_df_scaled, 3)
cluster_plot <- fviz_cluster(
list(data = random_df_scaled, cluster = km_res2$cluster),
ellipse.type = "convex", geom = "point", stand = F,
palette = "jco", ggtheme = theme_classic()
)
den_plot <- fviz_dend(
hclust(dist(random_df_scaled), method = "ward.D"), k = 3, k_colors = "jco",
as.gplot = T, show_labels = F
)
cluster_plot + den_plot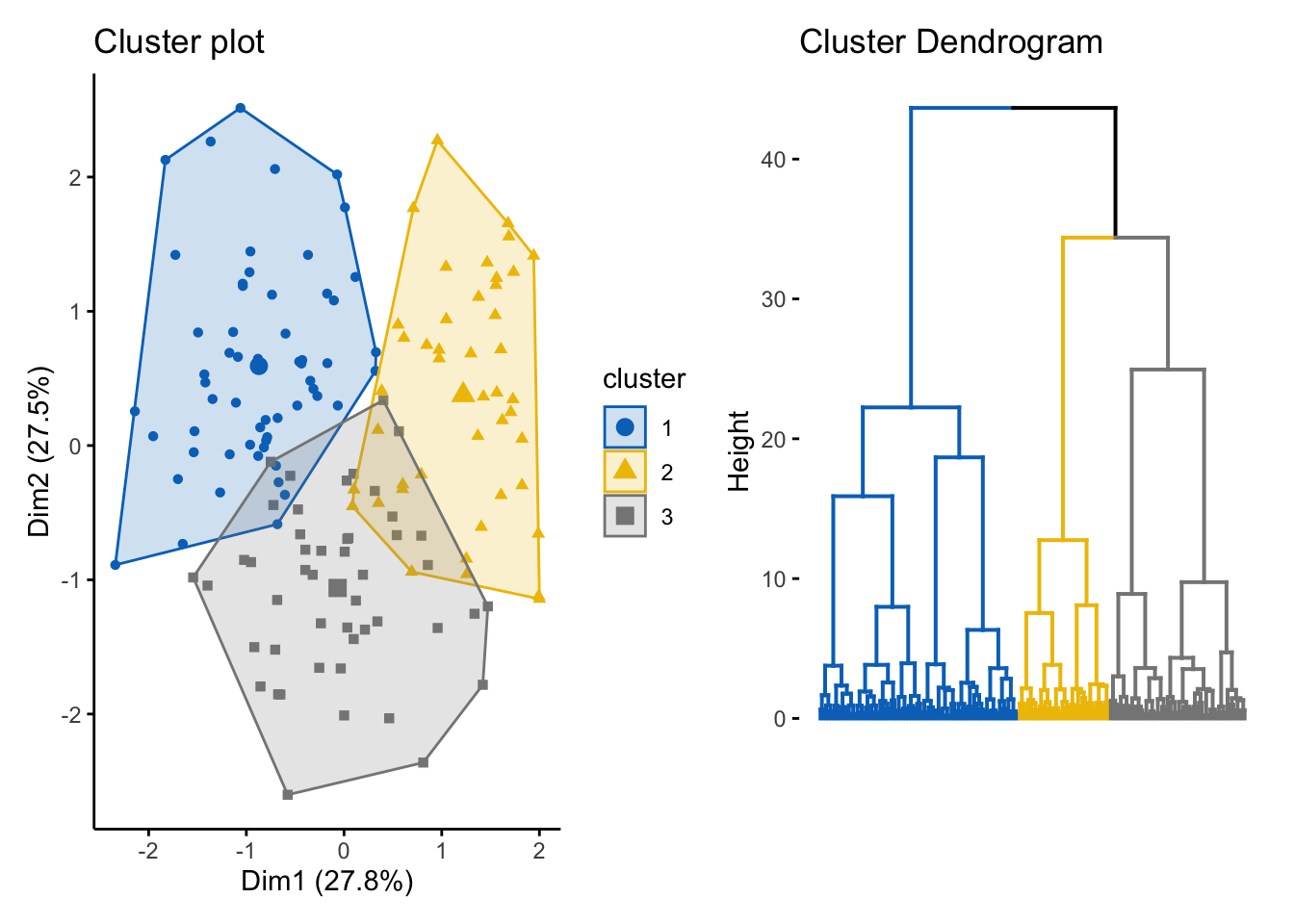
Puede observarse que ambos métodos imponen una segmentación a los datos que son uniformemente aleatorios y que no contienen ninguna segmentación natural. Por esta razón, siempre deberá realizarse este análisis previamente y elegir si se desea proceder con el análisis.
El método anterior fue totalmente gráfico. Se procede a continuación a mostrar una metodología estadística para determinar la factibilidad de implementar análisis de clustering.
El estadístico Hopkins es usado para evaluar la tendencia de clustering en un conjunto de datos. Mide la probabilidad de que un conjunto de datos dado sea generado por una distribución uniforme. En otras palabras, prueba la aleatoriedad espacial de los datos. Por ejemplo, Sea D un conjunto de datos real, el estadístico de Hopkins puede ser calculado de la siguiente forma:
Proceso:
Muestrear aleatoriamente n puntos \((p_1, p_2, p_3, ..., p_n)\) de D
Para cada punto \(p_i \in D\), encontrar su vecino más cercano \(p_j\); luego calcular la distancia entre \(p_i\) y \(p_j\) y denotarla como \(x_i = dist(p_i, p_j)\)
Generar un conjunto de datos simulado \((random_D)\) tomado de una distribución uniformemente aleatoria con n puntos \((q_1, q_2, q_3, ..., q_n)\) y de la misma variación que la original del conjunto D.
Para cada punto \(q_i \in random_D\), encontrar su vecino más cercano \(q_j\) en D; posteriormente, calcular la distancia entre \(q_i\) y \(q_j\) y denotarla como \(y_i=dist(q_i, q_j)\).
Calcular el estadístico de Hopkins como la distancia media más cercana de vecinos en los datos aleatorios y dividirlos por la suma de las distancias medias de vecinos más cercanos de los datos reales y aleatorios:
\[H=\frac{\sum_{i=1}^{n}{y_i}}{\sum_{i=1}^{n}{x_i} + \sum_{i=1}^{n}{y_i}}\]
Un valor cercano a 0.5 significa que \(\sum_{i=1}^{n}{y_i}\) y \(\sum_{i=1}^{n}{x_i}\) son similares uno del otro y por lo tanto, D es distribuida aleatoriamente.
Por lo tanto, las hipótesis nula y alternativa son definidas como sigue:
Hipótesis Nula: El conjunto de datos D es uniformemente distribuido (sin clusters significativos).
Hipótesis Alternativa: El conjunto de datos D no es distribuido uniformemente (contiene clusters significativos).
Cuando el estadístico de Hopkins tiene valores cercanos a cero, entonces puede rechazarse la hipótesis nula y concluir que el conjunto de datos D tiene datos conglomerables significativos.
library(hopkins)
set.seed(19735)
1 - hopkins::hopkins(df_scaled, nrow(df_scaled)-1, 4)## [1] 0.005107394Este valor sugiere rechazar la hipótesis nula en favor de la alternativa.
Por último, se compararán otros 2 gráficos con la disimilitud de los dos conjuntos de datos. La metodología de este gráfico lleva por nombre “Visual Assessment of Cluster Tendency” (VAT). Este método consiste de 3 pasos:
Calcula la matriz de disimilaridad (DM) entre objetos usando la distancia Euclidiana.
Re-ordena la DM de forma que los elementos similares estén cercanos unos de otros. Este proceso crea una Matriz de Di-similaridad Ordenada (ODM).
La ODM es mostrada como una imagen de disimilaridad ordenada, la cual es la salida visual de VAT.
dis_irirs_plot <- fviz_dist(
dist(df_scaled),
show_labels = FALSE) +
labs(title = "Iris data")
dis_random_plot <- fviz_dist(
dist(random_df_scaled),
show_labels = FALSE) +
labs(title = "Random data")
dis_irirs_plot + dis_random_plot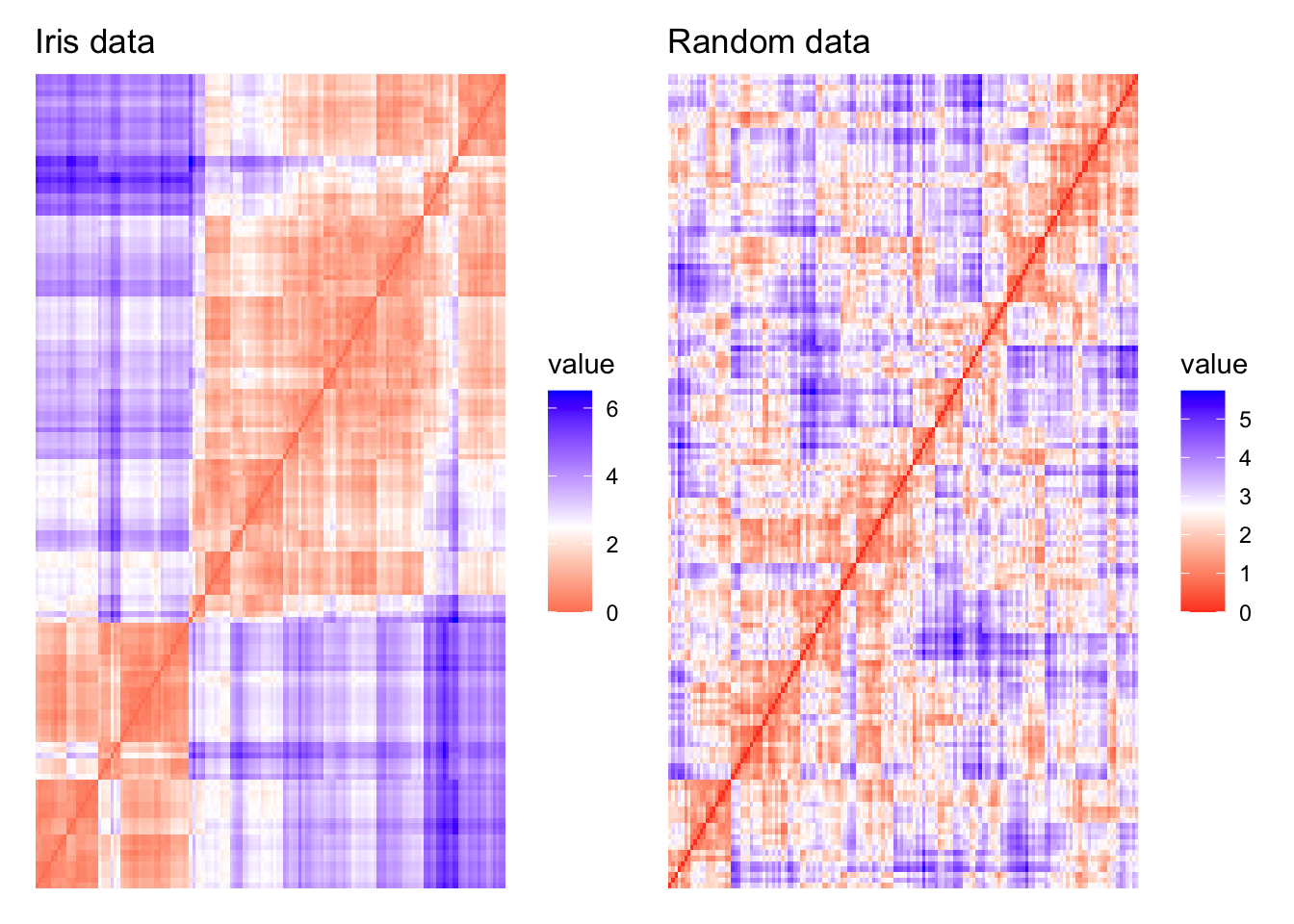
Donde:
Rojo: Alta similaridad
Azul: Baja similaridad
La matriz de disimilaridad anterior confirma que existe una estructura de cluster en el conjunto de datos Iris, pero no en el aleatorio.
La técnica VAT detecta la tendencia de clustering de forma visual al contar el número de bloques cuadradas sobre la diagonal en la imagen VAT.
9.3 K - means
La agrupación en grupos con K-means es uno de los algoritmos de aprendizaje de máquina no supervisados más simples y populares.
K-medias es un método de agrupamiento, que tiene como objetivo la partición de un conjunto de n observaciones en k grupos en el que cada observación pertenece al grupo cuyo valor medio es más cercano.
Un cluster se refiere a una colección de puntos de datos agregados a a un grupo debido a ciertas similitudes.
9.3.1 Ajuste de modelo: ¿Cómo funciona el algortimo?
- Paso 1: Seleccionar el número de clusters K
El primer paso en k-means es elegir el número de conglomerados, K. Como estamos en un problema de análisis no supervisado, no hay K correcto, existen métodos para seleccionar algún K pero no hay respuesta correcta.
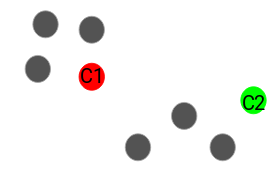
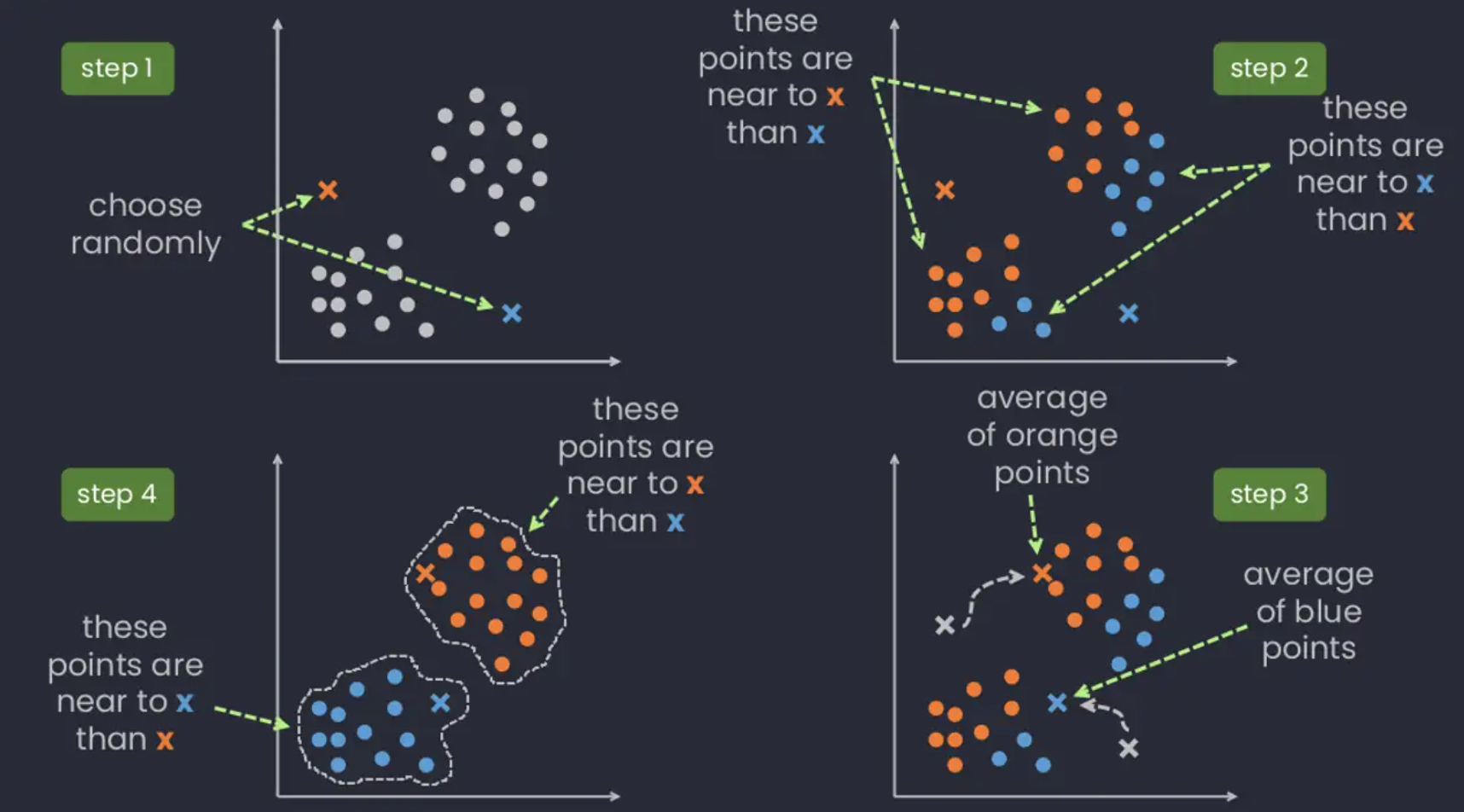
- Paso 2: Seleccionar K puntos aleatorios de los datos como centroides.
A continuación, seleccionamos aleatoriamente el centroide para cada grupo. Supongamos que queremos tener 2 grupos, por lo que K es igual a 2, seleccionamos aleatoriamente los centroides:
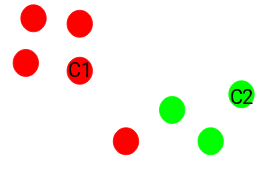
- Paso 3: Asignamos todos los puntos al centroide del cluster más cercano.
Una vez que hemos inicializado los centroides, asignamos cada punto al centroide del cluster más cercano:
- Paso 4: Volvemos a calcular los centroides de los clusters recién formados.
Ahora, una vez que hayamos asignado todos los puntos a cualquiera de los grupos, el siguiente paso es calcular los centroides de los grupos recién formados:
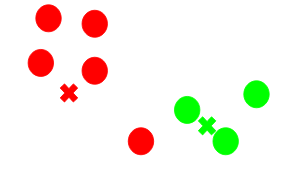
- Paso 5: Repetir los pasos 3 y 4.
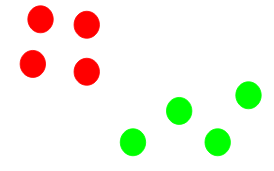
- Criterios de paro:
Existen tres criterios de paro para detener el algoritmo:
- Los centroides de los grupos recién formados no cambian:
Podemos detener el algoritmo si los centroides no cambian. Incluso después de múltiples iteraciones, si obtenemos los mismos centroides para todos los clusters, podemos decir que el algoritmo no está aprendiendo ningún patrón nuevo y es una señal para detener el entrenamiento.
- Los puntos permanecen en el mismo grupo:
Otra señal clara de que debemos detener el proceso de entrenamiento si los puntos permanecen en el mismo cluster incluso después de entrenar el algoritmo para múltiples iteraciones.
- Se alcanza el número máximo de iteraciones:
Finalmente, podemos detener el entrenamiento si se alcanza el número máximo de iteraciones. Supongamos que hemos establecido el número de iteraciones en 100. El proceso se repetirá durante 100 iteraciones antes de detenerse.
9.3.2 Calidad de ajuste
9.3.2.1 Inercia
La idea detrás de la agrupación de k-medias consiste en definir agrupaciones de modo que se minimice la variación total dentro de la agrupación (conocida como within cluster variation o inertia).
Existen distintos algoritmos de k-medias, el algoritmo estándar es el algoritmo de Hartigan-Wong, que define within cluster variation como la suma de las distancias euclidianas entre los elementos y el centroide correspondiente al cuadrado:
\[W(C_k)=\sum_{x_i \in C_k}(x_i-\mu_k)²\]
donde \(x_i\) es una observación que pertenece al cluster \(C_k\) y \(\mu_k\) es la media del cluster \(C_k\)
Cada observación \(x_i\) se asigna a un grupo de modo que la suma de cuadrados de la distancia de la observación a sus centroide del grupo asignado \(\mu_k\) es mínima.
Definimos la total within cluster variation total de la siguiente manera:
\[total \quad within = \sum_{k=1}^{K}W(C_k) = \sum_{k=1}^{K}\sum_{x_i \in C_k}(x_i-\mu_k)²\]
9.3.3 ¿Cómo seleccionamos K?
Una de las dudas más comunes que se tienen al trabajar con K-Means es seleccionar el número correcto de clusters.
El número máximo posible de conglomerados será igual al número de observaciones en el conjunto de datos.
Pero entonces, ¿cómo podemos decidir el número óptimo de agrupaciones? Una cosa que podemos hacer es trazar un gráfico, también conocido como gráfica de codo, donde el eje x representará el número de conglomerados y el eje y será una métrica de evaluación, en este caso usaremos inertia.
Comenzaremos con un valor de K pequeño, digamos 2. Entrenaremos el modelo usando 2 grupos, calculamos la inercia para ese modelo y, finalmente, agregamos el punto en el gráfico mencionado. Digamos que tenemos un valor de inercia de alrededor de 1000:
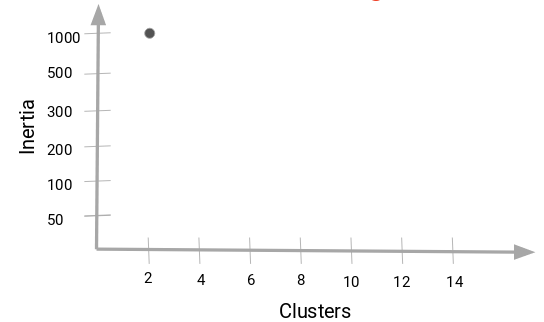
Ahora, aumentaremos el número de conglomerados, entrenaremos el modelo nuevamente y agregaremos el valor de inercia en la gráfica con distintos números de K:
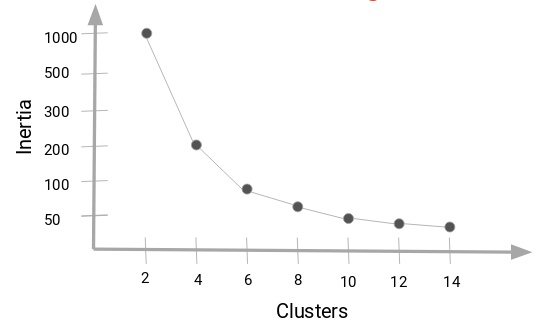
Cuando cambiamos el valor de K de 2 a 4, el valor de inercia se redujo de forma muy pronunciada. Esta disminución en el valor de inercia se reduce y eventualmente se vuelve constante a medida que aumentamos más el número de grupos.
Entonces, el valor de K donde esta disminución en el valor de inercia se vuelve constante se puede elegir como el valor de grupo correcto para nuestros datos.
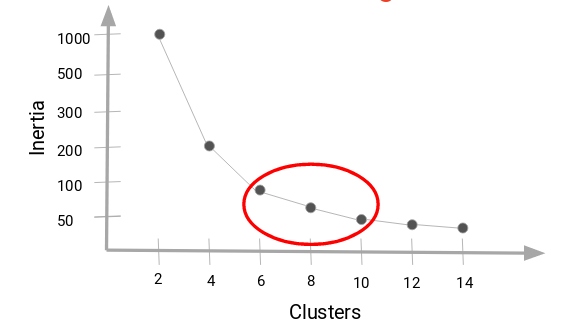
Aquí, podemos elegir cualquier número de conglomerados entre 6 y 10. Podemos tener 7, 8 o incluso 9 conglomerados. También debe tener en cuenta el costo de cálculo al decidir la cantidad de clusters. Si aumentamos el número de clusters, el costo de cálculo también aumentará. Entonces, si no tiene recursos computacionales altos, deberíamos un número menor de clusters.
9.3.4 Implementación en R
Usaremos los datos USArrests, que contiene estadísticas, en arrestos por cada 100,000 residentes por asalto, asesinato y violación en cada uno de los 50 estados de EE. UU. En 1973. También se da el porcentaje de la población que vive en áreas urbanas.
data("USArrests")
head(USArrests)## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7df <-scale(USArrests, center = T, scale = T)
df <- na.omit(df)
head(df, n = 5)## Murder Assault UrbanPop Rape
## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
## Arizona 0.07163341 1.4788032 0.9989801 1.042878388
## Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
## California 0.27826823 1.2628144 1.7589234 2.067820292Usaremos la función kmeans(), los siguientes parámetros son los más usados:
X: matriz numérica de datos, o un objeto que puede ser forzado a tal matriz (como un vector numérico o un marco de datos con todas las columnas numéricas).
centers: ya sea el número de conglomerados(K), o un conjunto de centros de conglomerados iniciales (distintos). Si es un número, se elige un conjunto aleatorio de observaciones (distintas) en x como centros iniciales.
iter.max: el número máximo de iteraciones permitido.
nstart: si centers es un número, ¿cuántos conjuntos aleatorios deben elegirse?
algorithm: Algoritmo a usar
En el siguiente ejemplo se agruparán los datos en seis grupos (centers = 6). Como se había mencionado, la función kmeans también tiene una opción nstart que intenta múltiples configuraciones iniciales y regresa la mejor, agregar nstart = 25 generará 25 configuraciones iniciales.
k6 <- kmeans(df, centers = 6, nstart = 25)La salida de kmeans es una lista con distinta información. La más importante:
cluster: Un vector de números enteros (de 1:K) que indica el grupo al que se asigna cada punto.
centers: una matriz de centros.
totss: La suma total de cuadrados.
withinss: Vector de suma de cuadrados dentro del grupo, un componente por grupo.
tot.withinss: Suma total de cuadrados dentro del conglomerado, es decir, sum(withinss)
betweenss: La suma de cuadrados entre grupos, es decir, \(totss-tot.withinss\).
size: el número de observaciones en cada grupo.
También podemos ver nuestros resultados usando la función fviz_cluster(). Esto proporciona una ilustración de los grupos. Si hay más de dos dimensiones (variables), fviz_cluster() realizará un análisis de componentes principales (PCA) y trazará los puntos de datos de acuerdo con los dos primeros componentes principales que explican la mayor parte de la varianza.
library(factoextra)
fviz_cluster(k6, data = df, ellipse.type = "t", repel = TRUE)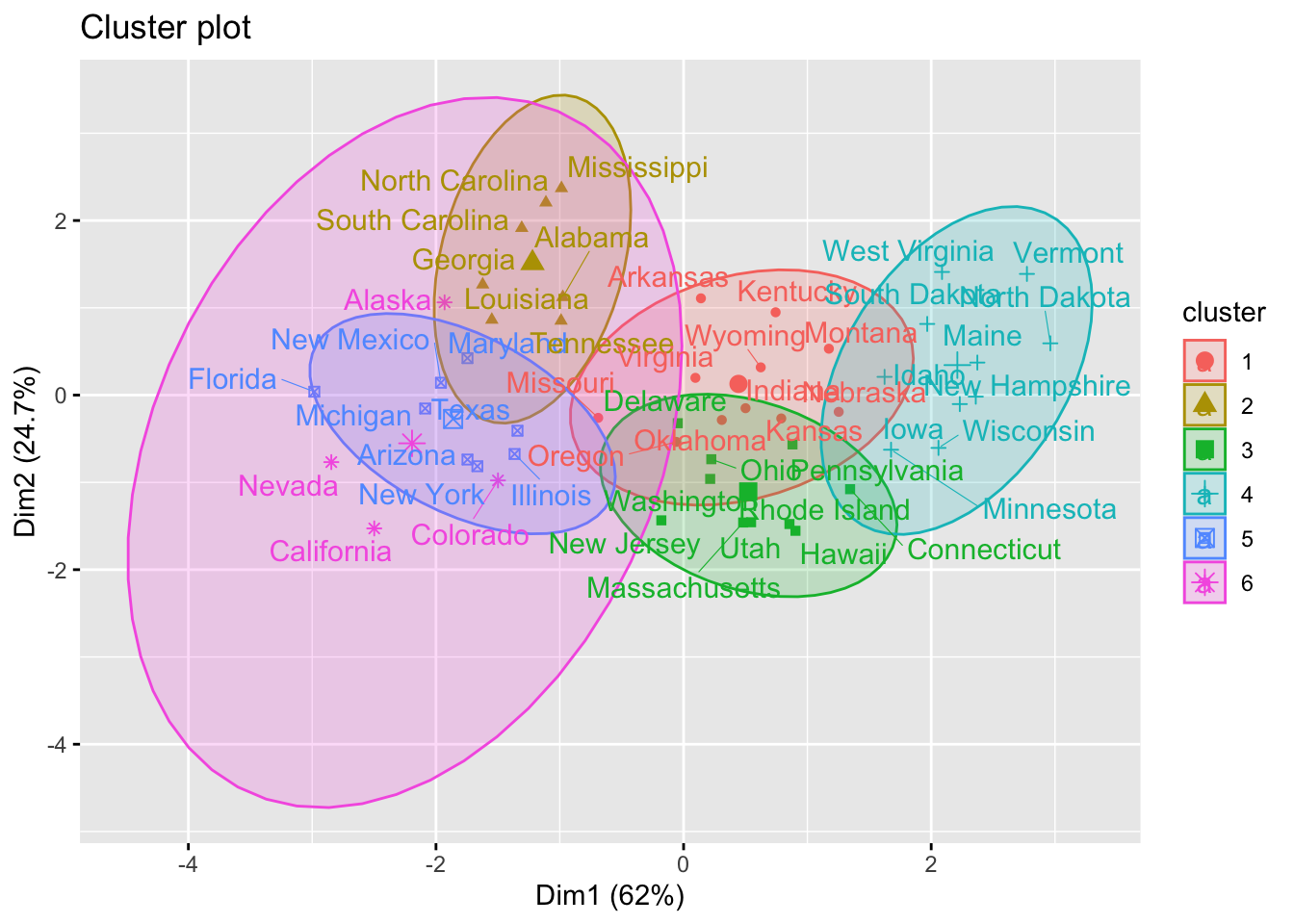
Debido a que el número de conglomerados (K) debe establecerse antes de iniciar el algoritmo, a menudo es recomendado utilizar varios valores diferentes de K y examinar las diferencias en los resultados. Podemos ejecutar el mismo proceso para 3, 4 y 5 clusters, y los resultados se muestran en la siguiente figura:
library(patchwork)
library(gridExtra)
k2 <- kmeans(df, centers = 2, nstart = 25)
k3 <- kmeans(df, centers = 3, nstart = 25)
k4 <- kmeans(df, centers = 4, nstart = 25)
k5 <- kmeans(df, centers = 5, nstart = 25)
p2 <- fviz_cluster(k2, geom = "point", ellipse.type = "t", data = df) + ggtitle("K = 2")
p3 <- fviz_cluster(k3, geom = "point", ellipse.type = "t", data = df) + ggtitle("K = 3")
p4 <- fviz_cluster(k4, geom = "point", ellipse.type = "t", data = df) + ggtitle("K = 4")
p5 <- fviz_cluster(k5, geom = "point", ellipse.type = "t", data = df) + ggtitle("K = 5")
grid.arrange(p2, p3, p4, p5, nrow = 2)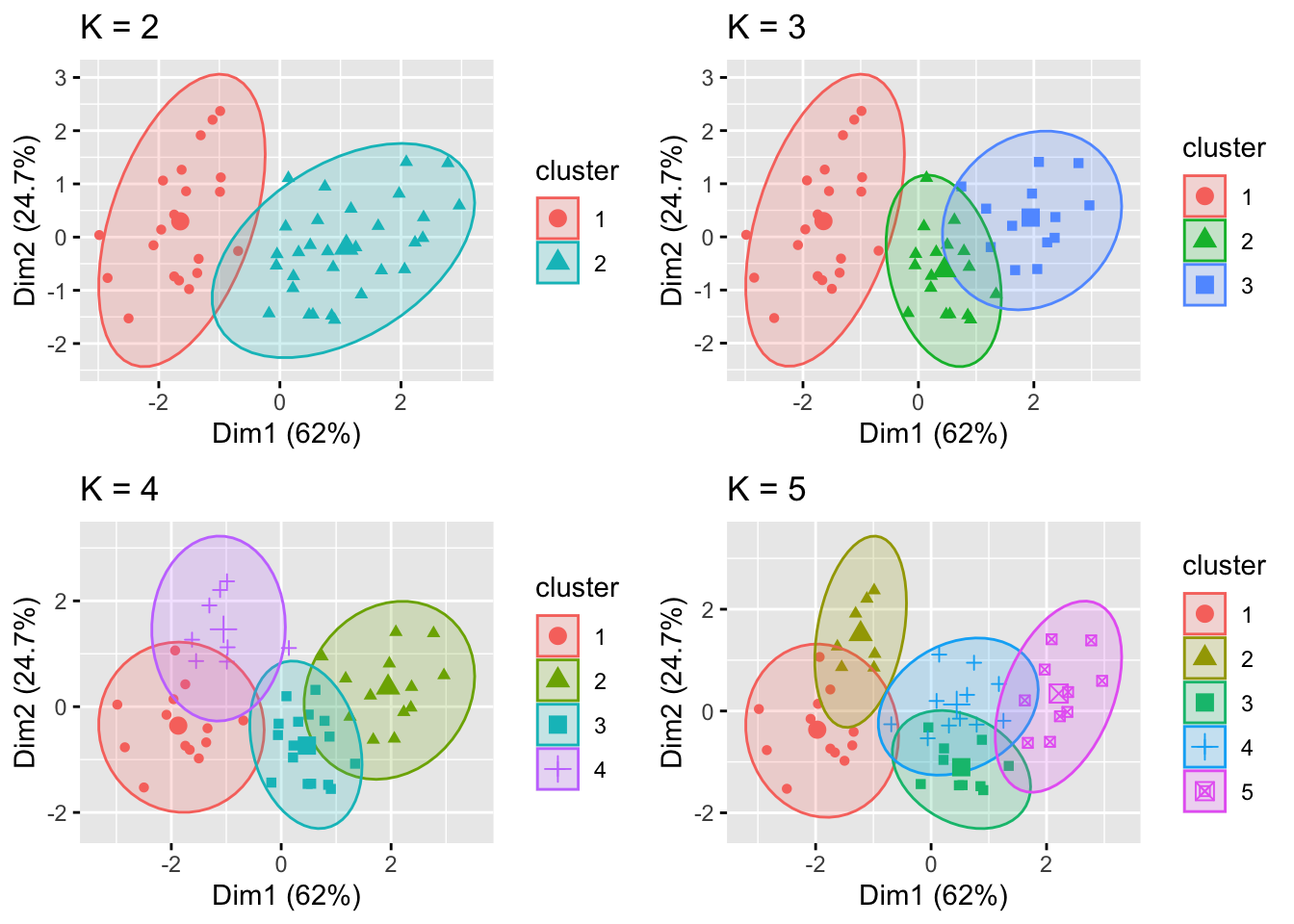
Recordemos que podemos usar la gráfica de codo para obtener el número óptimo de K, usaremos la función fviz_nbclust() para esto.
set.seed(123)
wss_plot <- fviz_nbclust(df, kmeans, method = "wss")
wss_plot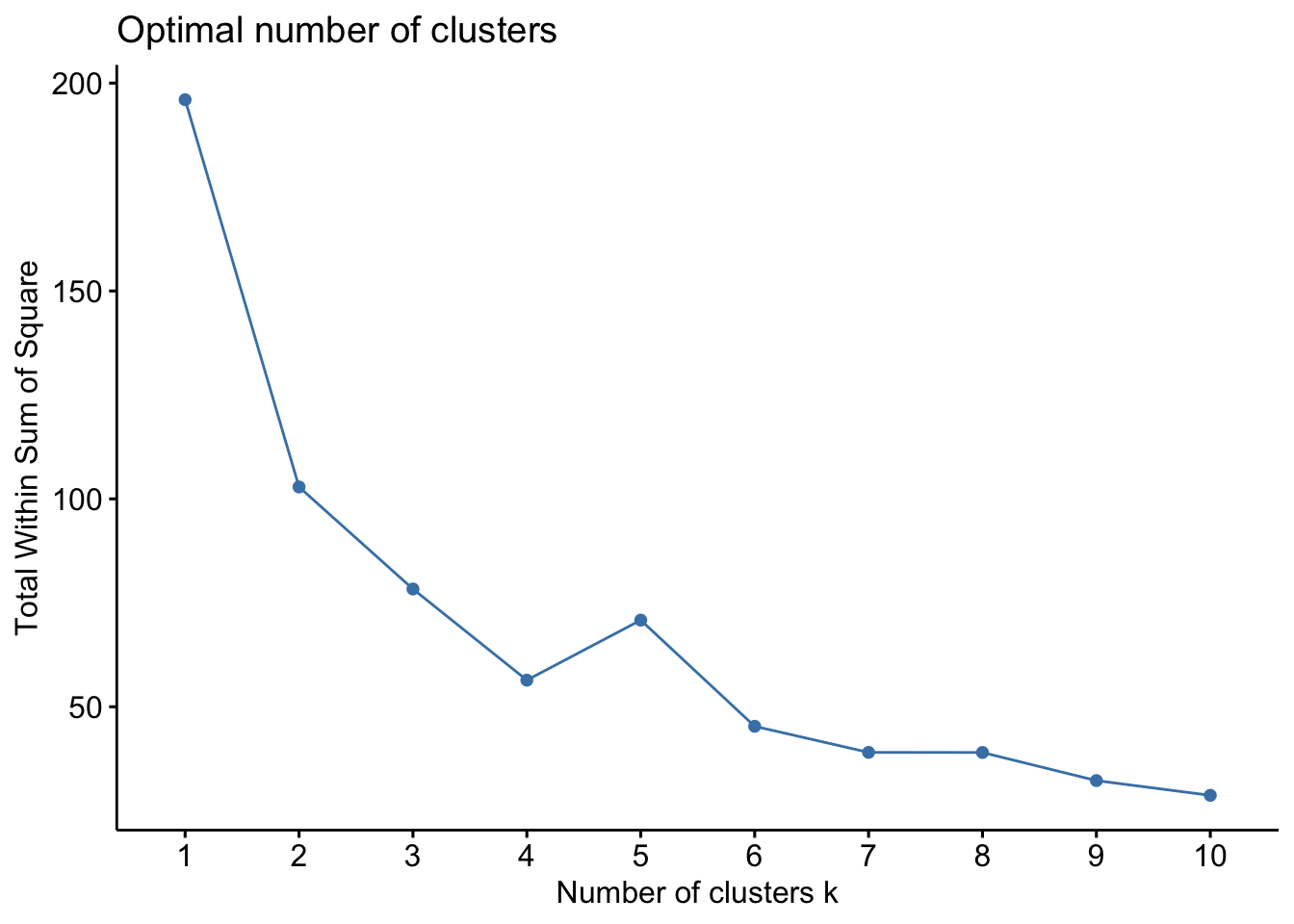
set.seed(123)
final <- kmeans(df, 2, nstart = 25)kmeans_plot <- fviz_cluster(
final,
data = df,
ellipse.type = "t",
repel = TRUE) +
ggtitle("K-Means Plot") +
theme_minimal() +
theme(legend.position = "bottom")
kmeans_plot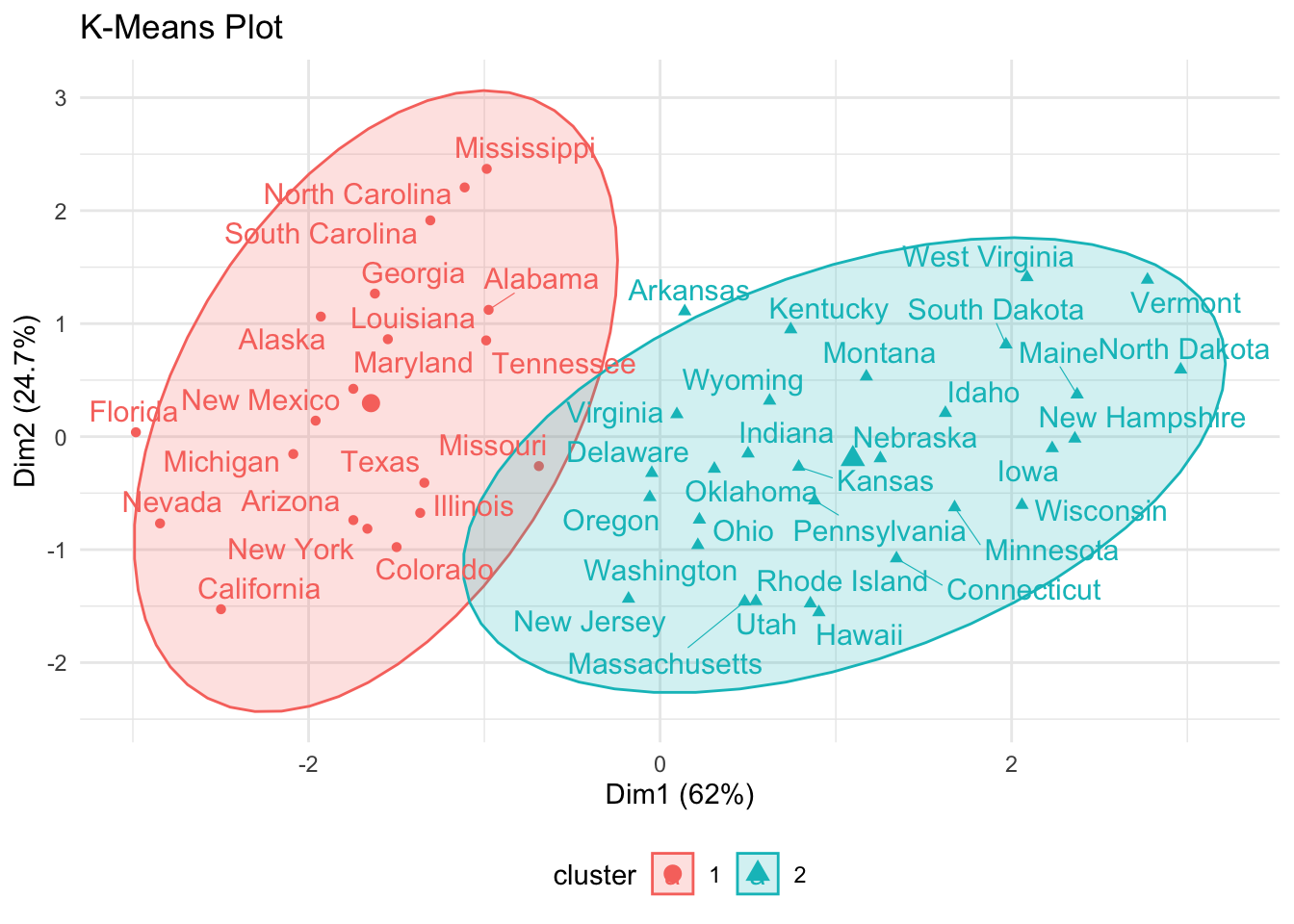
9.3.5 Warnings
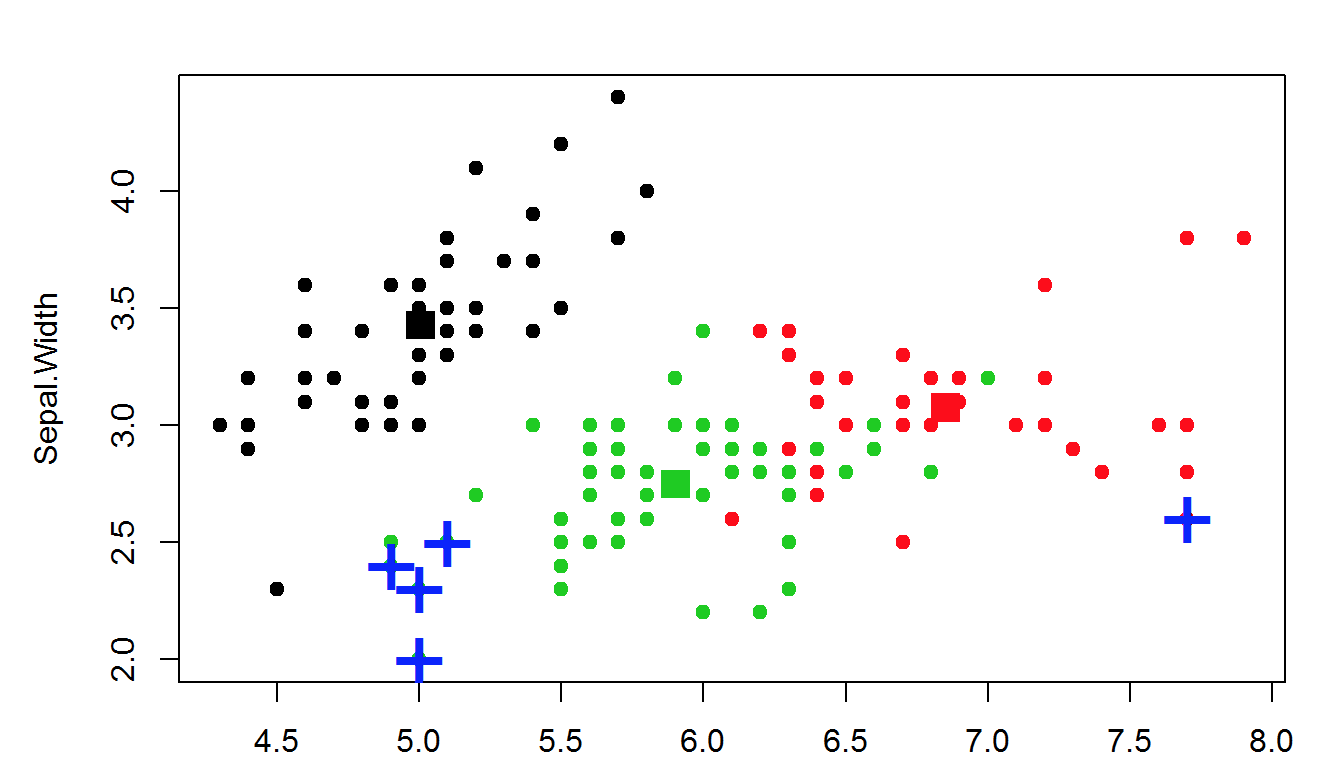
Dado que este algoritmo está basado en promedios, debe de ser considerada su sensibilidad a valores atípicos, esto es, si un valor esta lejos del resto, el centroide de un cluster puede cambiar drásticamente y eso significa que también puede incluir dentro del mismo grupo a puntos diferentes de los que de otra manera no serían incluidos en ese conglomerado.
9.4 Partitioning Around Medoids (PAM)
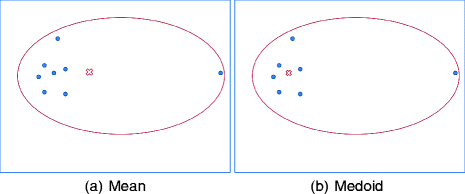
El algoritmo k-medoides es un enfoque de agrupamiento para particionar un conjunto de datos en k grupos o clusters. En k-medoides, cada grupo está representado por uno de los puntos de datos pertenecientes a un grupo. Estos puntos son nombrados medoides.
El término medoide se refiere a un objeto dentro de un grupo para el cual la disimilitud promedio entre él y todos los demás miembros del cluster son mínimos. Corresponde a el punto más céntrico del grupo.
Este algoritmo es una alternativa sólida de k-medias. Debido a que este algoritmo es menos sensible al ruido y los valores atípicos, en comparación con k-medias, pues usa medoides como centros de conglomerados en lugar de medias. El uso de medias implica que la agrupación de k-medias es muy sensible a los valores atípicos, lo cual puede afectar gravemente la asignación de observaciones a los conglomerados.
El método de agrupamiento de k-medoides más común es el algoritmo PAM (Partitioning Around Medoids, Kaufman & Rousseeuw, 1990).
9.4.1 Algoritmo PAM
El algoritmo PAM se basa en la búsqueda de k objetos representativos o medoides entre las observaciones del conjunto de datos. Después de encontrar un conjunto de k medoides, los grupos se construyen asignando cada observación al medoide más cercano. Posteriormente, cada medoide m y cada punto de datos no medoide seleccionado se intercambian y se calcula la función objetivo.
La función objetivo corresponde a la suma de las disimilitudes de todos los objetos a su medoide más cercano.
El objetivo es encontrar k objetos representativos que minimicen la suma de disimilitudes de las observaciones con su objeto representativo más cercano. Como se mencionó anteriormente, el algoritmo PAM funciona con una matriz de disimilitud y para calcular esta matriz, el algoritmo puede utilizar dos métricas:
La distancia euclidiana, que es la raíz de la suma de cuadrados de las diferencias;
Y la distancia de Manhattan, que es la suma de distancias absolutas.
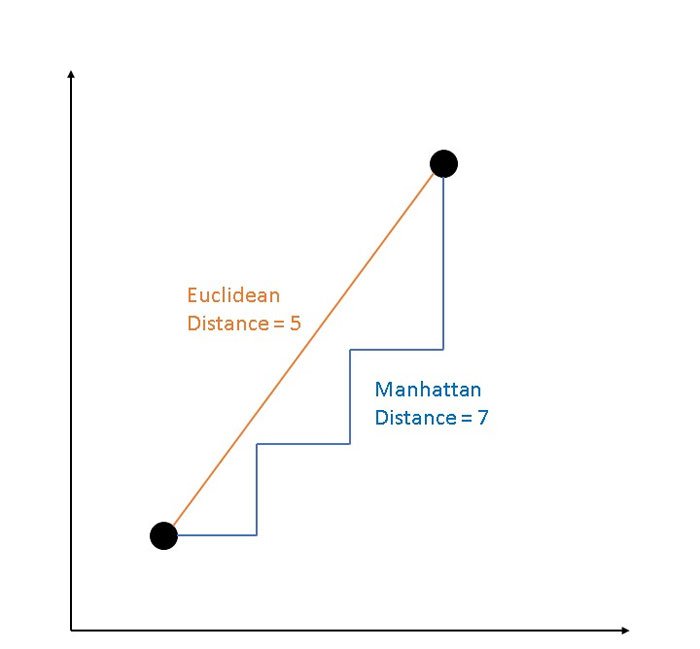
Nota: En la práctica, se debería obtener resultados similares la mayor parte del tiempo, utilizando cualquiera de estas distancias mencionadas. Si lo datos contienen valores atípicos, distancia de Manhattan debería dar resultados más sólidos, mientras que la distancia euclidiana se vería influenciada por valores inusuales.
9.4.2 Implementación en R
Para estimar el número óptimo de clusters, usaremos el método de silueta promedio. La idea es calcular el algoritmo PAM utilizando diferentes valores de los conglomerados k. Después, la silueta promedio de los conglomerados se dibuja de acuerdo con el número de conglomerados.
La silueta media mide la calidad de un agrupamiento. Una silueta media alta indica una buena agrupación.
El número óptimo de conglomerados k es el que maximiza la silueta promedio sobre un rango de valores posibles para k
La función fviz_nbclust() del paquete factoextra proporciona una solución conveniente para estimar el número óptimo de conglomerados con diferentes métodos.
library(cluster)
# Elbow method
Elbow <- fviz_nbclust(df, pam, method = "wss") +
geom_vline(xintercept = 4, linetype = 2)+
labs(subtitle = "Elbow method")
Elbow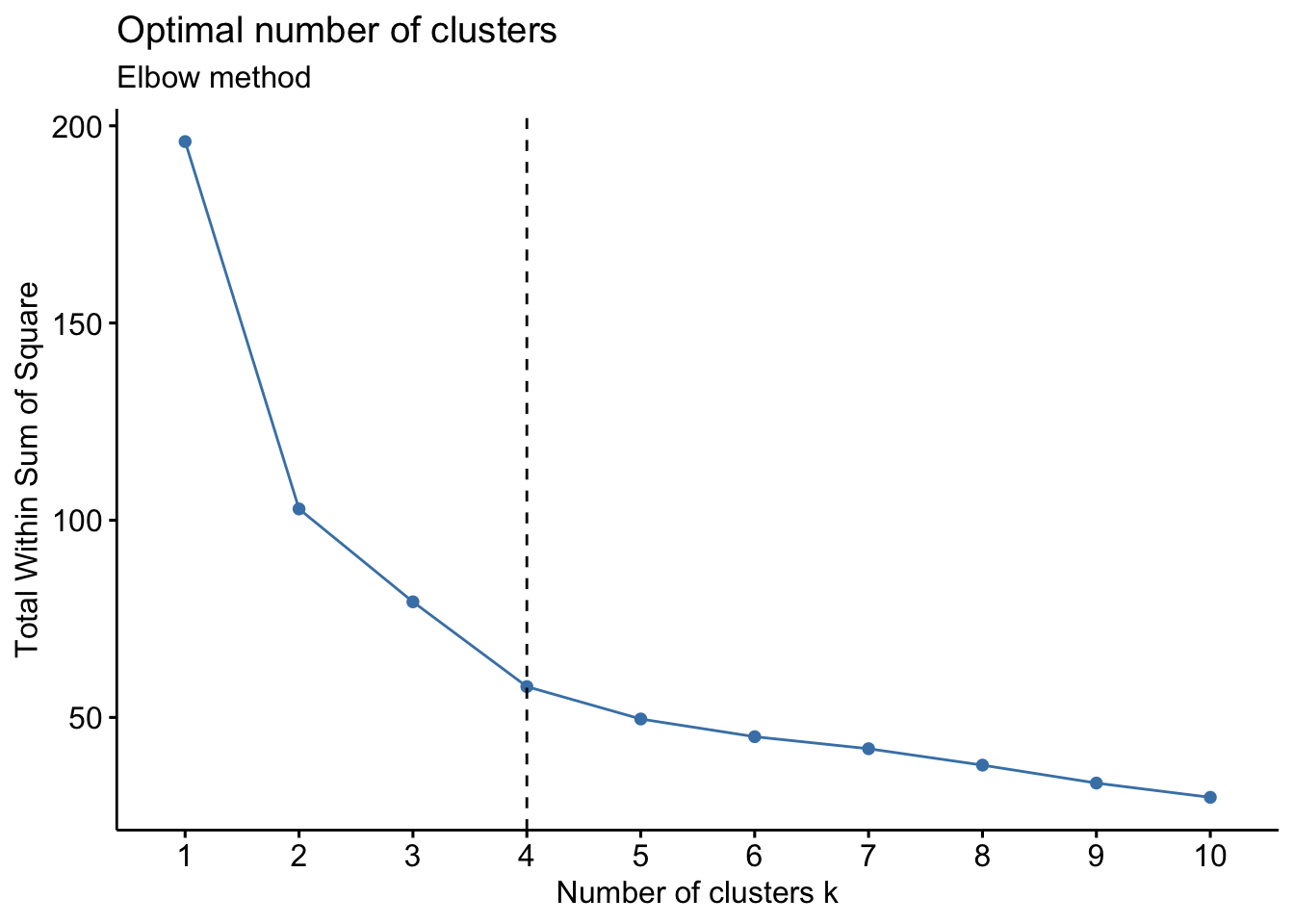
¿Qué se hace en estos casos?
Es importante conocer las diferencias entre cada grupo y entender si este resultado tiene sentido desde un enfoque de negocio. Una vez entendiendo la razón por la cual 9 grupos es viable desde múltiples criterios, se deberá tomar la decisión del número adecuado de grupos.
Otro criterio importante, es entender los índices y su interpretación. Conocer el significado de cada índice será importante para conocer la validez de su uso y consideración.
A partir de la gráfica se observa que la cantidad sugerida de grupos es 2 o 9, por lo que en la siguiente sección se clasificarán las observaciones en 2 grupos.
La función pam() del paquete Cluster se puede utilizar para calcular
PAM.
k_mediods <- pam(df, 2)
print(k_mediods)## Medoids:
## ID Murder Assault UrbanPop Rape
## New Mexico 31 0.8292944 1.3708088 0.3081225 1.1603196
## Nebraska 27 -0.8008247 -0.8250772 -0.2445636 -0.5052109
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 1 1 1 2 1
## Colorado Connecticut Delaware Florida Georgia
## 1 2 2 1 1
## Hawaii Idaho Illinois Indiana Iowa
## 2 2 1 2 2
## Kansas Kentucky Louisiana Maine Maryland
## 2 2 1 2 1
## Massachusetts Michigan Minnesota Mississippi Missouri
## 2 1 2 1 1
## Montana Nebraska Nevada New Hampshire New Jersey
## 2 2 1 2 2
## New Mexico New York North Carolina North Dakota Ohio
## 1 1 1 2 2
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 2 2 2 2 1
## South Dakota Tennessee Texas Utah Vermont
## 2 1 1 2 2
## Virginia Washington West Virginia Wisconsin Wyoming
## 2 2 2 2 2
## Objective function:
## build swap
## 1.441358 1.368969
##
## Available components:
## [1] "medoids" "id.med" "clustering" "objective" "isolation"
## [6] "clusinfo" "silinfo" "diss" "call" "data"La salida impresa muestra:
Los medoides del grupo: una matriz, cuyas filas son los medoides y las columnas son variables
El vector de agrupación: un vector de números enteros (de \(1:k\)) que indica la agrupación a que se asigna a cada punto
Para visualizar los resultados de la partición, usaremos la función fviz_cluster() del paquete factoextra.
Esta función dibuja un diagrama de dispersión de puntos de datos coloreados por números de grupo. Si los datos contienen más de 2 variables, se utiliza el algoritmo de análisis de componentes principales (PCA) para reducir la dimensionalidad de los datos. En este caso, los dos primeros componentes se utilizan para trazar los datos.
pam_plot <- fviz_cluster(
k_mediods,
palette = c("#00AFBB", "#FC4E07"),
ellipse.type = "t",
repel = TRUE,
ggtheme = theme_minimal()) +
ggtitle('K-Medoids Plot') +
theme(legend.position = "bottom")
pam_plot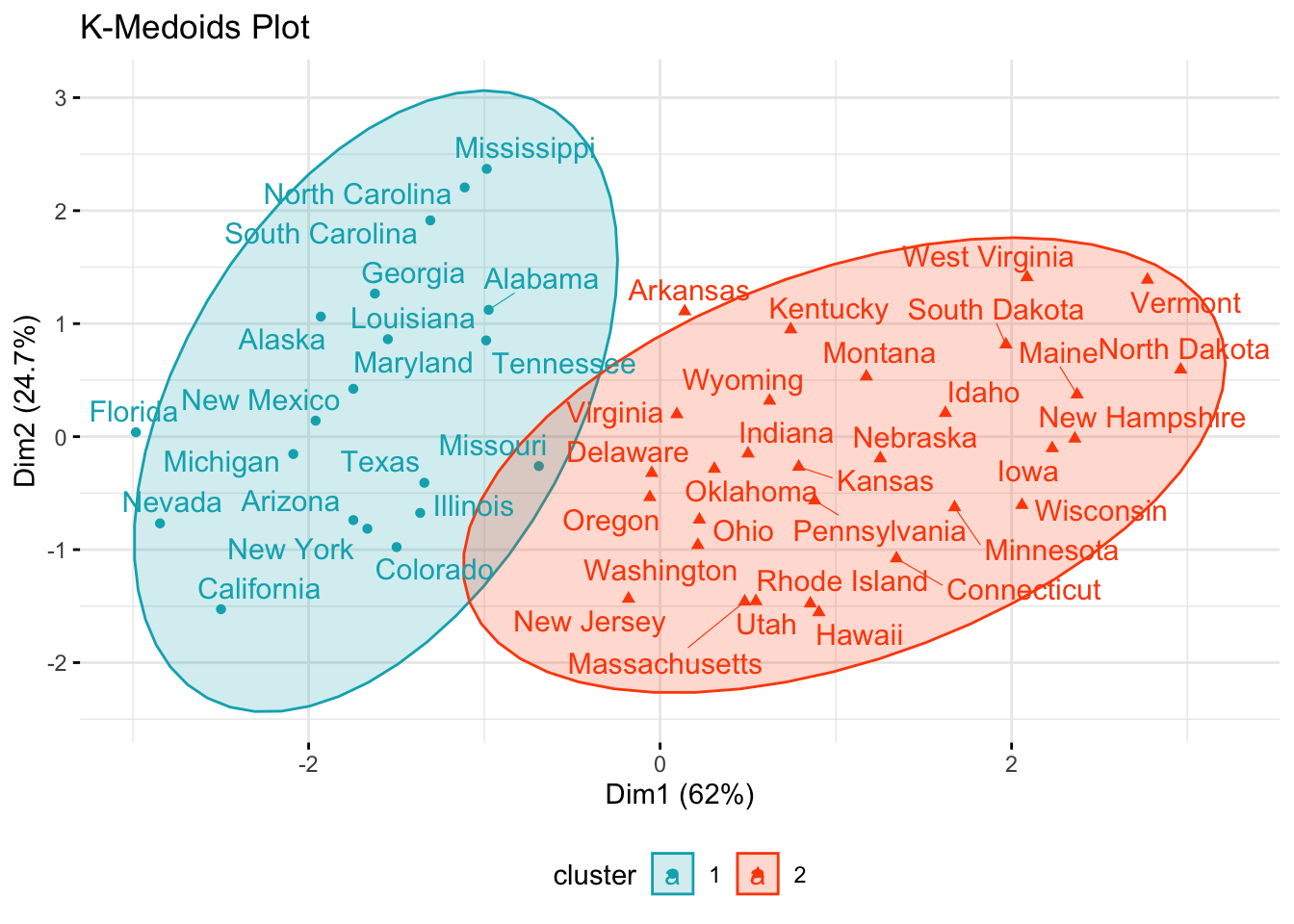
Ejercicio:
Calcular los centroides de cada grupo realizando 2 segmentaciones
Calcular los centroides de cada grupo realizando 9 segmentaciones
Comparar los resultados anteriores y comentar
9.5 Comparación de algoritmos
Un buen análisis de clustering no sucede sin antes comparar los resultados producidos por los distintos algoritmos. A continuación, se presenta la comparación de las gráficas. Esta comparación visual sirve de apoyo para conocer las diferencias entre los distintos métodos, sin embargo, esto no sustituye al análisis numérico de wss, silhouette o algún otro.
kmeans_plot + pam_plot 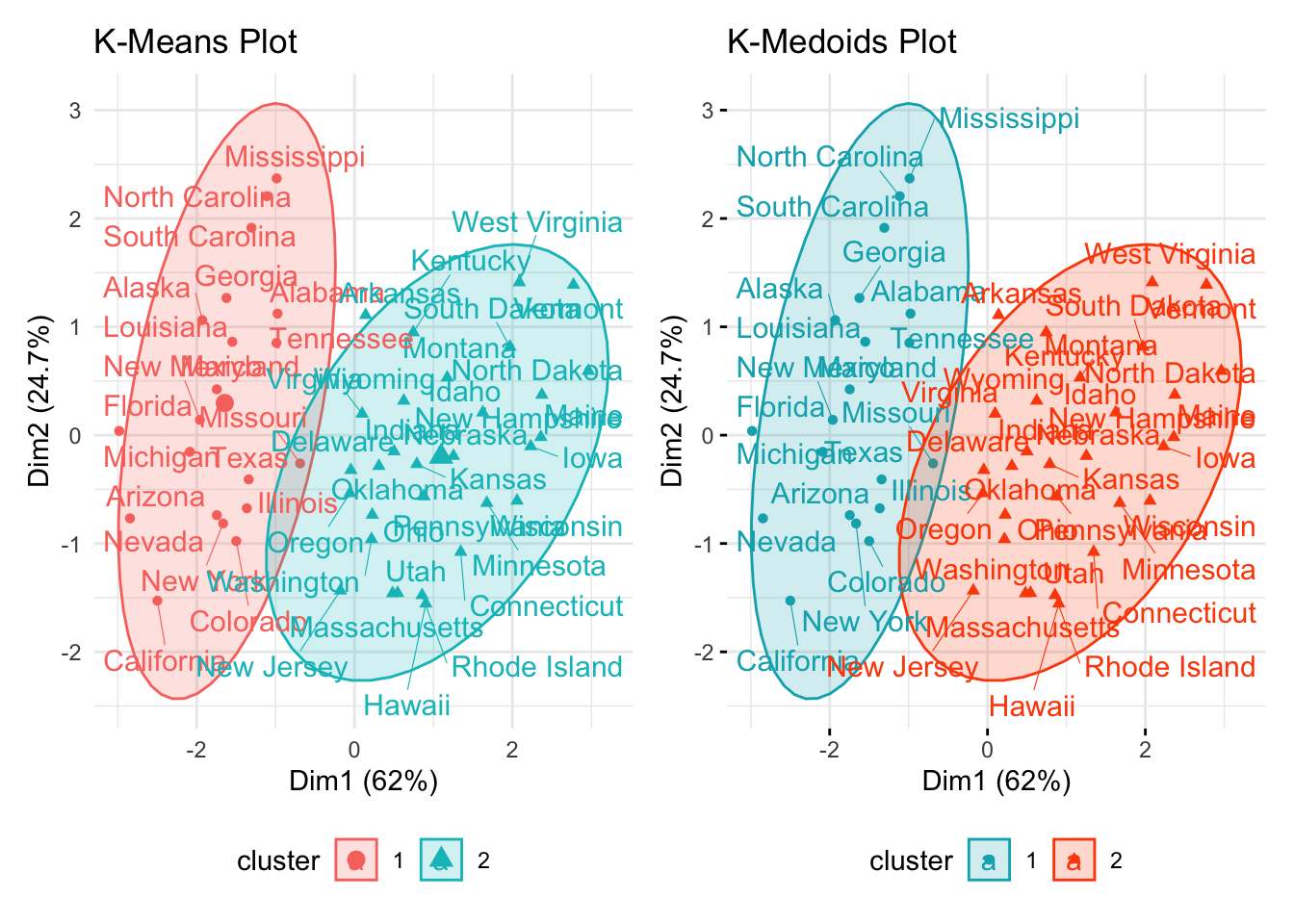
Ejercicio
Comparar el grado de marginación original de CONAPO con los distintos algoritmos de clustering revisados hasta el momento.